题目内容
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,点E在BC上,点F在AB的延长线上,且AE=CF.

(1)求证:△ABE≌△CBF.
(2)若∠ACF=70°,求∠EAC的度数.
【答案】(1)见解析;(2)∠EAC=20°
【解析】
(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠FBC的度数,又由Rt△ABE≌Rt△CBF,即可求得∠EAB的度数,再得出∠EAC即可求得答案.
证明:∵∠ABC=90°
∴△ABE与△CBF为直角三角形.
∵在Rt△ABE与Rt△BCF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF;
(2)∵AB=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵∠ACF=70°,
∴∠FBC=25°,
由Rt△ABE≌Rt△CBF,∴∠EAB=∠FBC=25°,
∴∠EAC=20°.

练习册系列答案
相关题目
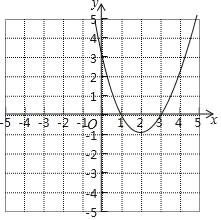
【题目】如图,已知在坐标平面内,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 在点
在点![]() 的正北方向
的正北方向![]() 个单位处,把点
个单位处,把点![]() 向上平移
向上平移![]() 个单位再向左平移
个单位再向左平移![]() 个单位得到点
个单位得到点![]() .
.
![]() 在下图中画出平面直角坐标系和
在下图中画出平面直角坐标系和![]() ,写出点
,写出点![]() 、点
、点![]() 的坐标;
的坐标;
![]() 在图中作出
在图中作出![]() 关于
关于![]() 轴的轴对称图形
轴的轴对称图形![]() ;
;
![]() 求出
求出![]() 的面积
的面积
【题目】如图,观察每个正多边形中![]() 的变化情况,解答下列问题:
的变化情况,解答下列问题:

(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | … | 15 |
| … |
(2)根据规律,是否存在一个正![]() 边形,使其中
边形,使其中![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)根据规律,是否存在一个正![]() 边形,使其中
边形,使其中![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.