题目内容
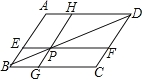
【题目】如图，在ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，则图中面积相等的平行四边形共有_____对．
【答案】3
【解析】
根据平行四边形的性质证全等三角形，然后利用等量关系推出面积相等．
解：∵四边形ABCD是平行四边形，
∴S△ABD＝S△CBD．
∵BP是平行四边形BEPG的对角线，
∴S△BEP＝S△BGP，
∵PD是平行四边形HPFD的对角线，
∴S△HPD＝S△FPD．
∴S△ABD﹣S△BEP﹣S△HPD＝S△BCD﹣S△BGP﹣S△PFD，即SAEPH＝SGCFP，
∴SABGH＝SBCFE，
同理SAEFD＝SGCDH．
即：SABGH＝SBCFE，SAHPE＝SGCFP，SAEFD＝SGCDH
故答案为：3.
练习册系列答案
华东师大版一课一练系列答案
相关题目
