Question

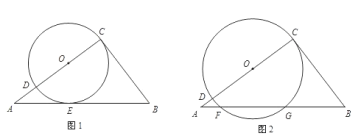
【题目】已知，Rt△ABC中，∠C=90°，AC=4，BC=3．以AC上一点O为圆心的⊙O与BC相切于点C，与AC相交于点D．

（1）如图1，若⊙O与AB相切于点E，求⊙O的半径；

（2）如图2，若⊙O在AB边上截得的弦FG= ， 求⊙O的半径．

Answer 1

【答案】(1) ⊙O的半径为;(2) ⊙O的半径为

【解析】

（1）由于AB和圆相切，所以连接OE，利用相似即可求出OE．
（2）已知弦长，求半径，要做弦的弦心距，构造直角三角形，利用勾股定理求出未知量．

解：（1）连接OE，

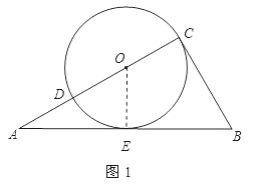
因为⊙O与AB相切于点E，所以OE⊥AB，

设OE=x，则CO=x，AO=4﹣x，

∵⊙O与AB相切于点E，

∴∠AEO=90°，

∵∠A=∠A，∠AEO=∠ACB=90°，

∴Rt△AOE∽Rt△ABC，

∴，

∴，

解得：x=，

∴⊙O的半径为．

（2）过点O作OH⊥AB，垂足为点H，则H为FG的中点，FH=FG=，

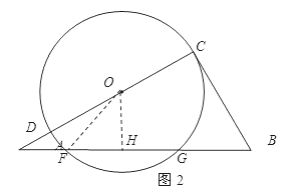
连接OF，设OF=x，则OA=4﹣x，

由Rt△AOH∽Rt△ABC可得OH=，

在Rt△OHF中，据勾股定理得：OF2=FH2+OH2 ，

∴x2=（）2+（）2 ，

解得x1=，x2=（舍去），

∴⊙O的半径为．