题目内容
已知圆半径为1,点P为圆外一点.AP切圆于点A,PA=1,AB为圆的弦,AB=
.求∠PAB的度数.
| 2 |
考点:切线的性质
专题:计算题
分析:连结OA、OB,如图,先根据勾股定理的逆定理得到△AOB为直角三角形,∠AOB=90°,则∠OAB=45°,再根据切线的性质得∠PAO=90°,然后分类讨论:当AP与AB在OA的两侧,则∠PAB=∠PAO+∠OAB;当AP与AB在OA的同侧,则∠PAB=∠PAO-∠OAB.
解答:解: 连结OA、OB,如图,
连结OA、OB,如图,
∵OA=1,OB=1,AB=
,
∴OA2+OB2=AB2,
∴△AOB为直角三角形,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠OAB=45°,
∵AP切圆于点A,
∴OA⊥PA,
∴∠PAO=90°,
当AP与AB在OA的两侧,则∠PAB=∠PAO+∠OAB=90°+45°=135°;
当AP与AB在OA的同侧,则∠PAB=∠PAO-∠OAB=90°-45°=45°;
综上所述,∠PAB的度数为45°或135°.
 连结OA、OB,如图,
连结OA、OB,如图,∵OA=1,OB=1,AB=
| 2 |
∴OA2+OB2=AB2,
∴△AOB为直角三角形,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠OAB=45°,
∵AP切圆于点A,
∴OA⊥PA,
∴∠PAO=90°,
当AP与AB在OA的两侧,则∠PAB=∠PAO+∠OAB=90°+45°=135°;
当AP与AB在OA的同侧,则∠PAB=∠PAO-∠OAB=90°-45°=45°;
综上所述,∠PAB的度数为45°或135°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了勾股定理的逆定理.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知
=
,则x的值是( )
| 3 |
| x |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
二次函数式y=x2-2x+3配方后,结果正确的是( )
| A、y=(x+1)2-2 |
| B、y=(x-1)2+2 |
| C、y=(x+2)2+3 |
| D、y=(x-1)2+4 |
 如图,已知AB∥CD,试再添上一个条件,使∠ABF=∠ECD成立.
如图,已知AB∥CD,试再添上一个条件,使∠ABF=∠ECD成立.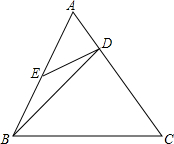 在等边△ABC中,点D、E分别在AC,AB上,且
在等边△ABC中,点D、E分别在AC,AB上,且