题目内容
2.小明晚上6点多外出购物,看手表上时针与分针的夹角为110°,接近7点回到家,发现时针与分针的夹角又是110°.问小明外出时用了多少时间?分析 根据题意,设小明外出到回家时针走了x°,则分针走了(2×110°+x°),可得到时针的度数,又因为时针每小时走30°,故小明外出用的时间可求.
解答 解:设时针从小明外出到回家走了x°,则分针走了(2×110°+x°),
由题意,得$\frac{220°+x°}{360°}$=$\frac{x°}{30°}$,
解得x=20°,
∵时针每小时走30°,
∴$\frac{20°}{30°}$=$\frac{2}{3}$小时,即小明外出用了40分钟时间.
点评 本题考查应用类问题,钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动($\frac{1}{12}$)°,并且利用起点时间时针和分针的位置关系建立方程求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
14.下列推理正确的是( )
| A. | 如果a=b,则ac=bc | |
| B. | 若a=b,则$\frac{a}{c}$=$\frac{b}{c}$ | |
| C. | 因为∠AOB=∠BOC,所以两角是对顶角 | |
| D. | 因为两角的和是180°,所以两角互为邻补角 |
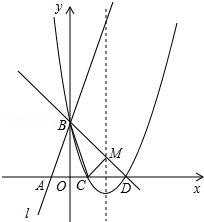 如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,一抛物线过点B、C和D,点D与点B关于直线y=x对称.
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,一抛物线过点B、C和D,点D与点B关于直线y=x对称.
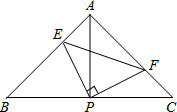 如图,在△ABC中,AB=AC,∠BAC=90°.直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( )
如图,在△ABC中,AB=AC,∠BAC=90°.直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=$\frac{1}{2}$S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有 ( )