题目内容
8.解方程(1)(x-2)(x-3)=(x+5)(x-1)+15
(2)$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$.
分析 (1)先化简得到-9x=4,再解一元一次方程即可;
(2)先把分式方程整理成整式方程,再按照解整式方程的步骤进行计算,最后再进行检验,即可得出答案.
解答 解:(1)(x-2)(x-3)=(x+5)(x-1)+15,
x2-5x+6=x2+4x-5+15,
-9x=4,
x=-$\frac{4}{9}$;
(2)$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$,
2(x+1)=4,
2x+2=4,
2x=2,
x=1,
经检验x=1是增根,
故原方程无解.
点评 此题考查了解分式方程和用解一元二次方程,解题的关键是掌握因式分解法的步骤和解分式方程的步骤,注意解分式方程一定要验根.

练习册系列答案
相关题目
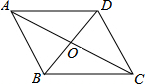 如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.
如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.