Question

6．如图，△ADB、△BCD都是等边三角形，点E，F分别是AB，AD上两个动点，满足AE=DF．连接BF与DE相交于点G，CH⊥BF，垂足为H，连接CG．已知DG=a，BG=b，CG=2GH且a、b满足下列关系：a²+b²=5，ab=2，
（1）求证：△ADE≌△DBF
（2）延长FB到点M，使得BM=DG，连结CM．先补全图，然后求出GH的长．

Answer 1

分析 （1）根据SAS即可判定两个三角形全等．
（2）如图，延长FB到点M，使得BM=DG，连结CM．首先证明△CDG≌△CBM，CG=CM，∠DCG=∠BCM，由∠DCB=60°，∠GCM=60°，推出CG=CM=GM=3，由此即可解决问题．

解答 （1）证明：∵△ADB和△BCD是等边三角形
∴∠DAE=∠BDF=60°，AD=BD，
在△DAE和△BDF中，
$\left\{\begin{array}{l}{AD=BD}\\{∠DAE=∠BDF}\\{AE=DF}\end{array}\right.$，
∴△ADE≌△DBF．

（2）解：如图，延长FB到点M，使得BM=DG，连结CM．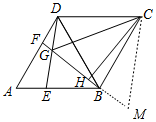

∵a²+b²=5，ab=2，
∴（a+b）²=a²+2ab+b²=5+4=9，
∵a+b＞0，
∴a+b=3，
由作图知，GM=GB+BM=GB+DG=a+b=3，
∠ADB+∠BDC=120°
∠DBF+∠CBM=120°
由（1）得，∠ADE=∠BDF
∴∠CDG=∠CBM
∴在△CDG  和△CBM中
$\left\{\begin{array}{l}{CD=CB}\\{∠CDG=∠CBM}\\{DG=BM}\end{array}\right.$，
∴△CDG≌△CBM，
∴CG=CM，∠DCG=∠BCM，
∵∠DCB=60°，∠GCM=60°
∴CG=CM=GM=3
又CG=2GH
∴GH=$\frac{3}{2}$．

点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会添加常用辅助线，属于中考常考题型．