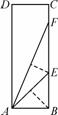
题目内容
如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
求证:AM⊥DF.

证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=45°,∠DCF=45°,∠ADC=90°,(2分)
在△ADE与△DCF中, ,∴△ADE≌△DCF(SAS),∠DAE=∠CDF.(6分)又∵∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°,
,∴△ADE≌△DCF(SAS),∠DAE=∠CDF.(6分)又∵∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°,
∴∠AMD=90°,即AM⊥DF.(10分)

练习册系列答案
相关题目

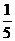 B.
B.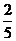 C.
C. D.
D.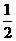


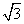 cm B.2
cm B.2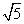 cm C.
cm C. cm D.
cm D.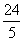 cm
cm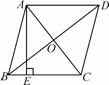
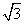 +1 B.
+1 B.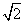 +1 C.2.5
+1 C.2.5  D.
D.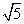
 的
的 解为( )
解为( ) 机抽取部分同
机抽取部分同
