题目内容
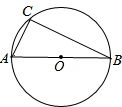如图，AB是⊙O的直径，已知该圆的半径为6.5cm，弦AC长5cm，求弦BC的长．考点：圆周角定理,勾股定理
专题：计算题
分析：先根据圆周角定理由AB是⊙O的直径得到∠C=90°，然后根据勾股定理计算BC的长．
解答：解：∵AB是⊙O的直径，
∴∠C=90°，
在Rt△ACB中，∵AB=13，AC=5，
∴BC=
=12，
即弦BC的长为12cm．
∴∠C=90°，
在Rt△ACB中，∵AB=13，AC=5，
∴BC=
| AB2-AC2 |
即弦BC的长为12cm．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了勾股定理．
练习册系列答案
相关题目
已知一次函数的y=（3m-1）x-m中，y随x的增大而减小，且函数图象不经过第一象限，则m的取值范围是（ ）
A、m＜
| ||
B、m＞
| ||
C、0≤m＜
| ||
| D、m＞0 |
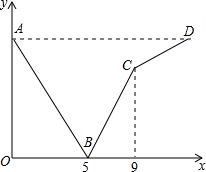一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，沿同一条道路匀速行驶，设行驶时间为t（h），两车之间的距离为s（km） 图中折线A-B-C-D表示s与t之间的函数关系．试通过计算说明，当快车到达乙地时，慢车还要多少时间才能到达甲地？
如图，一个正六棱柱高为10cm，底面正六边形的边长为3cm．