题目内容
用三种方法解方程:1+x+x2=73.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:计算题
分析:公式法:方程整理后,找出a,b,c的值,计算出根的判别式的值大于0,代入求根公式即可求出解;
配方法:方程变形后,利用完全平方公式变形,开方即可求出解;
因式分解法:方程整理后,左边化为积的形式,右边化为0,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
配方法:方程变形后,利用完全平方公式变形,开方即可求出解;
因式分解法:方程整理后,左边化为积的形式,右边化为0,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答:解:公式法:方程整理得:x2+x-72=0,
这里a=1,b=1,c=-72,
∵△=1+288=289,
∴x=
,
解得:x1=8,x2=-9;
配方法:方程变形得:x2+x=72,
配方得:x2+x+
=72
,即(x+
)2=
,
开方得:x+
=±
,
解得:x1=8,x2=-9;
因式分解法:方程整理得:x2+x-72=0,
分解因式得:(x-8)(x+9)=0,
解得:x1=8,x2=-9.
这里a=1,b=1,c=-72,
∵△=1+288=289,
∴x=
| -1±17 |
| 2 |
解得:x1=8,x2=-9;
配方法:方程变形得:x2+x=72,
配方得:x2+x+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 289 |
| 4 |
开方得:x+
| 1 |
| 2 |
| 17 |
| 2 |
解得:x1=8,x2=-9;
因式分解法:方程整理得:x2+x-72=0,
分解因式得:(x-8)(x+9)=0,
解得:x1=8,x2=-9.
点评:此题考查了解一元二次方程-因式分解法,公式法,以及配方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
若(m+1)2+|n-1|=0,则m2007+n2008的值是( )
| A、2008 | B、-2007 |
| C、1 | D、0 |
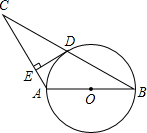 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D.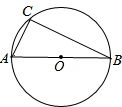 如图,AB是⊙O的直径,已知该圆的半径为6.5cm,弦AC长5cm,求弦BC的长.
如图,AB是⊙O的直径,已知该圆的半径为6.5cm,弦AC长5cm,求弦BC的长.