题目内容
解下列方程.
①2(x-3)2=x2-9(分解因式法)
②(x-2)(3x-5)=1(用公式法)
①2(x-3)2=x2-9(分解因式法)
②(x-2)(3x-5)=1(用公式法)
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:计算题
分析:(1)先把方程变形为2(x-3)2-(x+3)(x-3)=0,然后利用因式分解法化为x-3=0或2x-6-x-3=0,再分别解两个一次方程即可;
(2)先把方程化为一般式,再计算出判别式的值,然后利用求根公式求解.
(2)先把方程化为一般式,再计算出判别式的值,然后利用求根公式求解.
解答:解:(1)2(x-3)2-(x+3)(x-3)=0,
(x-3)(2x-6-x-3)=0,
x-3=0或2x-6-x-3=0,
所以x1=3,x2=9;
(2)方程化为3x2-11x+9=0,
△=112-4×3×9=13,
x=
所以x1=
,x2=
.
(x-3)(2x-6-x-3)=0,
x-3=0或2x-6-x-3=0,
所以x1=3,x2=9;
(2)方程化为3x2-11x+9=0,
△=112-4×3×9=13,
x=
11±
| ||
| 2×3 |
所以x1=
11+
| ||
| 6 |
11-
| ||
| 6 |
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.也考查了公式法解一元二次方程.

练习册系列答案
相关题目
如图图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
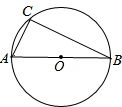 如图,AB是⊙O的直径,已知该圆的半径为6.5cm,弦AC长5cm,求弦BC的长.
如图,AB是⊙O的直径,已知该圆的半径为6.5cm,弦AC长5cm,求弦BC的长. 观察思考:
观察思考: