题目内容
 如图,一个正六棱柱高为10cm,底面正六边形的边长为3cm.
如图,一个正六棱柱高为10cm,底面正六边形的边长为3cm.(1)求这个正六棱柱的侧面积;
(2)若小蚂蚁沿六棱柱侧面爬,从顶点A爬到顶点B最短距离是多少?
考点:平面展开-最短路径问题
专题:
分析:(1)正六棱柱的侧面展开图是一个长方形,其中长为底面周长,宽为正六棱柱的高,根据长方形的面积公式计算即可;
(2)最短路线可放在平面内根据两点之间线段最短去求解,蚂蚁爬的两个面可以放平面内成为一个长方形,根据勾股定理去求解.
(2)最短路线可放在平面内根据两点之间线段最短去求解,蚂蚁爬的两个面可以放平面内成为一个长方形,根据勾股定理去求解.
解答: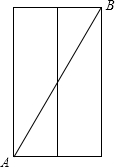 解:(1)将正六棱柱的侧面展开,得到一个长方形,此长方形的长=3×6=18,宽=10,
解:(1)将正六棱柱的侧面展开,得到一个长方形,此长方形的长=3×6=18,宽=10,
所以这个正六棱柱的侧面积=18×10=180(cm2);
(2)如图,将左侧面与正面展开,放在同一平面内,则小蚂蚁从顶点A爬到顶点B的最短距离为线段AB的长.
由勾股定理,得AB=
=2
(cm).
 解:(1)将正六棱柱的侧面展开,得到一个长方形,此长方形的长=3×6=18,宽=10,
解:(1)将正六棱柱的侧面展开,得到一个长方形,此长方形的长=3×6=18,宽=10,所以这个正六棱柱的侧面积=18×10=180(cm2);
(2)如图,将左侧面与正面展开,放在同一平面内,则小蚂蚁从顶点A爬到顶点B的最短距离为线段AB的长.
由勾股定理,得AB=
| (3+3)2+102 |
| 34 |
点评:此题考查了平面展开-最短路径问题,解决立体图形问题,一般都是根据题意把立体图形展开成平面图形,再在平面图形上解决问题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
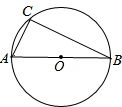 如图,AB是⊙O的直径,已知该圆的半径为6.5cm,弦AC长5cm,求弦BC的长.
如图,AB是⊙O的直径,已知该圆的半径为6.5cm,弦AC长5cm,求弦BC的长. 我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形.并利用差的符号来确定它们的大小,即要比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形.并利用差的符号来确定它们的大小,即要比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N. 观察思考:
观察思考: 如图,平面上有四个点A、B、C、D,根据下列语句画图
如图,平面上有四个点A、B、C、D,根据下列语句画图