题目内容
4.已知关于x的一元二次方程x2-(m-3)x-m=0(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且x12+x22-x1x2=7,求m的值.
分析 (1)要证明方程有两个不相等的实数根,只要证明原来的一元二次方程的△的值大于0即可;
(2)根据根与系数的关系可以得到关于m的方程,从而可以求得m的值.
解答 (1)证明:∵x2-(m-3)x-m=0,
∴△=[-(m-3)]2-4×1×(-m)=m2-2m+9=(m-1)2+8>0,
∴方程有两个不相等的实数根;
(2)∵x2-(m-3)x-m=0,方程的两实根为x1、x2,且x12+x22-x1x2=7,
∴$({x}_{1}+{x}_{2})^{2}-3{x}_{1}{x}_{2}=7$,
∴(m-3)2-3×(-m)=7,
解得,m1=1,m2=2,
即m的值是1或2.
点评 本题考查根与系数的关系、根的判别式,解答本题的关键是明确题意,找出所求问题需要的条件,利用方程的思想解答.

练习册系列答案
相关题目
12.据统计,参加南充市2016年高中阶段学校招生考试的人数为55354人,这个数用科学记数法表示为( )
| A. | 0.55354×105人 | B. | 5.5354×105人 | C. | 5.5354×104人 | D. | 55.354×103人 |
9.380亿用科学记数法表示为( )
| A. | 38×109 | B. | 0.38×1013 | C. | 3.8×1011 | D. | 3.8×1010 |
16. AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C;连接BC,若∠P=40°,则∠B等于( )
AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C;连接BC,若∠P=40°,则∠B等于( )
 AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C;连接BC,若∠P=40°,则∠B等于( )
AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C;连接BC,若∠P=40°,则∠B等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
13.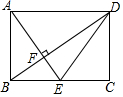 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
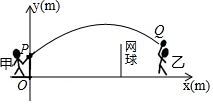 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m. 某班体育委员对本班学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是11小时.
某班体育委员对本班学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是11小时.