题目内容
6.先分解因式(1)(2)(3),再解答后面的问题.(1)1+a+a(1+a).
(2)1+a+a(1+a)+a(1+a)2
(3)1+a+a(1+a)+a(1+a)2+a(1+a)3
问题:
I.先探索上述分解因式的规律,再写出:1+a(1+a)+a(1+a)2+a(1+a)3+…+a(1+a)2014分解因式的结果是(1+a)2015.
Ⅱ.请按上述方法分解因式:1+a(1+a)+a(1+a)2+a(1+a)3+…+a(1+a)n(n为正整数).
分析 (1)提取公因式(1+a)即可得出答案;
(2)提取公因式(1+a),再结合同底数幂的乘法运算法则即可得出答案;
(3)提取公因式(1+a)再结合同底数幂的乘法运算法则即可得出答案;
I.根据以上规律即可得出运算规律,得出答案即可;
Ⅱ.根据以上规律即可得出运算规律,得出答案即可.
解答 解:(1)原式=(1+a)(1+a)=(1+a)2;
(2)原式=(1+a)[1+a+a(1+a)]=(1+a)(1+a)(1+a)=(1+a)3;
(3)原式=(1+a)[1+a+a(1+a)+a(1+a)2]
=(1+a)(1+a)[1+a+a(1+a)]
=(1+a)2(1+a)(1+a)
=(1+a)4,
Ⅰ.(1+a)2015,
故答案为:(1+a)2015;
Ⅱ.原式=(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-1]
=(1+a)(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-2]
=(1+a)2(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-3]
=(1+a)n-1(1+a)(1+a)=(1+a)n+1.
点评 此题主要考查了提取公因式法分解因式,根据运算结果得出规律是解题的关键.

练习册系列答案
相关题目
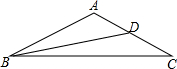 如图,△ABC中,AB=AC,BD是∠B的平分线.
如图,△ABC中,AB=AC,BD是∠B的平分线. 根据图中标明的尺寸,用含a的代数式表示图中阴影部分的面积为$\frac{π-2}{2}$a2(结果保留π)
根据图中标明的尺寸,用含a的代数式表示图中阴影部分的面积为$\frac{π-2}{2}$a2(结果保留π) 如图,在△ABC中,∠CAB=120°,AB=AC=4,∠BAC的平分线交BC于D,DF∥AB交∠BAD的平分线于F,则DF=2.
如图,在△ABC中,∠CAB=120°,AB=AC=4,∠BAC的平分线交BC于D,DF∥AB交∠BAD的平分线于F,则DF=2.