题目内容
16.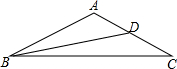 如图,△ABC中,AB=AC,BD是∠B的平分线.
如图,△ABC中,AB=AC,BD是∠B的平分线.(1)设∠ADB的度数为m,∠A的度数为n,求4m+3n的值.
(2)如果∠A=100°,求证:AD+BD=BC.
分析 (1)根据等腰三角形的性质得到∠ABC=∠C=$\frac{180°-n}{2}$,由角平分线的定义得到$∠DBC=\frac{1}{2}$∠ABC=$\frac{180°-n}{4}$,然后根据外角的性质列方程即可得到结果;
(2)以BC为边作等边三角形A'BC,在A'C上截取CD'=BD,连接A'A延长交BC于H,易证△ABD≌△ACD',可得AD=AD',∠BAC=∠CAD′=100°,即可求得A'D'=AD',即可解题.
解答 (1)解:∵AB=AC,
∴∠ABC=∠C=$\frac{180°-n}{2}$,
∵BD是∠B的平分线,
∴$∠DBC=\frac{1}{2}$∠ABC=$\frac{180°-n}{4}$,
∵∠ADB=∠C+∠DBC,
∴$\frac{180°-n}{2}$+$\frac{180°-n}{4}$=m,
∴4m+3n=540°;
(2)证明:以BC为边作等边三角形A'BC,在A'C上截取CD'=BD,连接A'A延长交BC于H,
∵A'B=A'C,AB=AC,
∴A'H是BC垂直平分线,∠D'A'A=30°,
∵AB=AC,∠BAC=100°,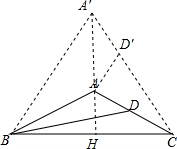
∴∠ACA′=∠ABD=20°,
在△ABD和△ACD'中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABD=∠ACD′}\\{BD=CD′}\end{array}\right.$,
∴△ABD≌△ACD'(SAS),
∴AD=AD',∠BAC=∠CAD′=100°,
∴∠AD′C=60°,连接AA′,
∴∠D'A'A=∠A'AD'=30°,
∴A'D'=AD',
∴BC=A'C=A'D'+CD'=AD+BD,
即BC=BD+AD.
点评 本题考查了等腰三角形的性质,全等三角形的判定和性质,角平分线的定义,本题中求证△ABD≌△ACD'是解题的关键.

| A. | a•b | B. | a+b | C. | 3a+b | D. | 3ab |
 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论: 如图,△ABC中,AB=AC,∠BAC=90°,D为AB垂直平分线上一点,∠DAC=30°,求∠BCD的度数.
如图,△ABC中,AB=AC,∠BAC=90°,D为AB垂直平分线上一点,∠DAC=30°,求∠BCD的度数.