题目内容
当m= 时,方程(m-2)x2-(m2-4)x+1=0的两根互为相反数.
考点:根与系数的关系,一元二次方程的定义
专题:
分析:先根据一元二次方程的定义和根与系数的关系得到m-2≠0,且m2-4=0,解得m=-2,然后根据根的判别式确定m的值.
解答:解:根据题意得m-2≠0,且m2-4=0,
解得m=-2.
因为m=-2时,原方程变形为-4x2+1=0,△=0+16>0,符合题意.
所以m=-2.
故答案为-2.
解得m=-2.
因为m=-2时,原方程变形为-4x2+1=0,△=0+16>0,符合题意.
所以m=-2.
故答案为-2.
点评:本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了一元二次方程的定义.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
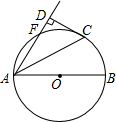 如图,AB是⊙O的直径,点F,C是⊙O上两点,且
如图,AB是⊙O的直径,点F,C是⊙O上两点,且
 如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于
如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于 将-2.5,-(-4),2,0,-|-3.5|在数轴上表示出来,并用“<”把这些数连接起来.
将-2.5,-(-4),2,0,-|-3.5|在数轴上表示出来,并用“<”把这些数连接起来. 已知:如图,⊙O中,直径AB⊥弦CD于点E,且CD=24,BE=8,求⊙O的半径.
已知:如图,⊙O中,直径AB⊥弦CD于点E,且CD=24,BE=8,求⊙O的半径.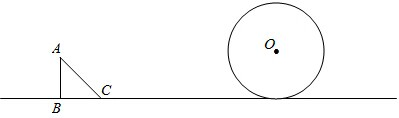
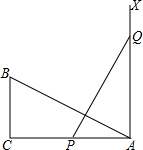 如图,有一个直角三角形ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到
如图,有一个直角三角形ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到