题目内容
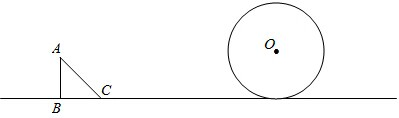
已知Rt△ABC和⊙O如图放置,已知AB=
,BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,设△ABC移动的时间为t(s).
(1)当△ABC的边AC与圆第一次相切时,求t的值;
(2)若在△ABC移动的同时,圆O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切时,求t的值;
(3)在(2)的条件下的移动过程中,圆心O到AC所在直线的距离在不断变化,设该距离为d,当d<1时,求t的取值范围.
| 3 |
(1)当△ABC的边AC与圆第一次相切时,求t的值;
(2)若在△ABC移动的同时,圆O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切时,求t的值;
(3)在(2)的条件下的移动过程中,圆心O到AC所在直线的距离在不断变化,设该距离为d,当d<1时,求t的取值范围.

考点:圆的综合题
专题:综合题
分析:(1)先根据含30度的直角三角形三边的关系得到∠A=30°,∠ACB=60°,作OD⊥直线BC,则OD=1,当△ABC的边AC与圆第一次相切时,如图1,△ABC平移到△A′B′C′的位置,A′C′与⊙O相切,作OE⊥A′C′,连接OC′,根据切线长定理得到∠OC′D=60°,在Rt△ODC′中计算出C′D=
,然后利用线段之间的关系得到2t+1+
=5,再解一次方程即可;
(2)如图2,△ABC从开始移动,到它的边与圆最后一次相切,即△ABC平移到△A′B′C′的位置,A′B′与⊙相切,作O′Q⊥A′B′于Q,由切线的性质得O′Q=1,则D′B′=1,然后利用线段之间的关系得到5+t+1=2t,再解一次方程即可;
(3)利用直线AC与圆两次相切的时间确定d<1时,t的范围:当△ABC平移到△A1B1C1的位置,A1C1与⊙O相切,d=1,如图3,由(1)得C1D=
,则DB1=DD′-B1C1-C1D′=t-1-
,利用线段之间的关系得5+t-1-
=2t,得到此时t=4-
;当△ABC平移到△A2B2C2的位置,A2C2与⊙O相切,d=1,如图3,作O′H⊥A2C2于H,根据切线长定理得到∠O′C2D′=30°,则C2D′=
O′D′=
,利用线段之间的关系得4+t+
=2t,得到此时t=4+
,于是当d<1时,t的取值范围为4-
<t<4+
.
| ||
| 3 |
| ||
| 3 |
(2)如图2,△ABC从开始移动,到它的边与圆最后一次相切,即△ABC平移到△A′B′C′的位置,A′B′与⊙相切,作O′Q⊥A′B′于Q,由切线的性质得O′Q=1,则D′B′=1,然后利用线段之间的关系得到5+t+1=2t,再解一次方程即可;
(3)利用直线AC与圆两次相切的时间确定d<1时,t的范围:当△ABC平移到△A1B1C1的位置,A1C1与⊙O相切,d=1,如图3,由(1)得C1D=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
解答:解:(1)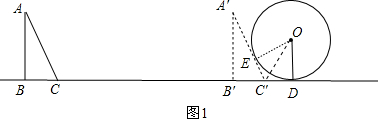 ∵AB=
∵AB=
,BC=1,∠ABC=90°,
∴AC=
=2,
∴∠A=30°,∠ACB=60°,
作OD⊥直线BC,则OD=1,
当△ABC的边AC与圆第一次相切时,如图1,△ABC平移到△A′B′C′的位置,A′C′与⊙O相切,作OE⊥A′C′,连接OC′,则OC′平分∠DC′E,
∵∠A′C′B′=∠ACB=60°,
∴∠OC′D=60°,
在Rt△ODC′中,∵OD=1,∠DOC′=30°,
∴C′D=
,
∵BB′=2t,B′C′=BC=1,BD=5,
∴2t+1+
=5,
∴t=2-
;
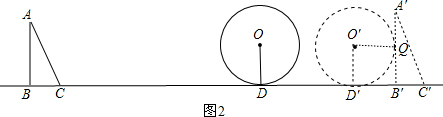 (2)如图2,△ABC从开始移动,到它的边与圆最后一次相切,即△ABC平移到△A′B′C′的位置,A′B′与⊙相切,作O′Q⊥A′B′于Q,
(2)如图2,△ABC从开始移动,到它的边与圆最后一次相切,即△ABC平移到△A′B′C′的位置,A′B′与⊙相切,作O′Q⊥A′B′于Q,
则O′Q=1,
∴D′B′=1,
∵BD=5,DD′=t,BB′=2t,
∴5+t+1=2t,
∴t=6;
(3)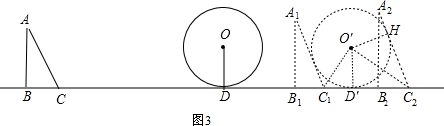 当△ABC平移到△A1B1C1的位置,A1C1与⊙O相切,d=1,如图3,由(1)得C1D=
当△ABC平移到△A1B1C1的位置,A1C1与⊙O相切,d=1,如图3,由(1)得C1D=
,
∵BD=5,DD′=t,BB1=2t,
∴DB1=DD′-B1C1-C1D′=t-1-
,
∴5+t-1-
=2t,
∴t=4-
;
当△ABC平移到△A2B2C2的位置,A2C2与⊙O相切,d=1,如图3,
作O′H⊥A2C2于H,
∵O′C2平分∠A2C2B2,
∴∠O′C2D′=30°,
∴C2D′=
O′D′=
,
∵CD+DD′+D′C2=CC2,
∴4+t+
=2t,
∴t=4+
,
∴当d<1时,t的取值范围为4-
<t<4+
.
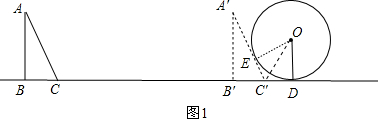 ∵AB=
∵AB=| 3 |
∴AC=
| AB2+BC2 |
∴∠A=30°,∠ACB=60°,
作OD⊥直线BC,则OD=1,
当△ABC的边AC与圆第一次相切时,如图1,△ABC平移到△A′B′C′的位置,A′C′与⊙O相切,作OE⊥A′C′,连接OC′,则OC′平分∠DC′E,
∵∠A′C′B′=∠ACB=60°,
∴∠OC′D=60°,
在Rt△ODC′中,∵OD=1,∠DOC′=30°,
∴C′D=
| ||
| 3 |
∵BB′=2t,B′C′=BC=1,BD=5,
∴2t+1+
| ||
| 3 |
∴t=2-
| ||
| 6 |
 (2)如图2,△ABC从开始移动,到它的边与圆最后一次相切,即△ABC平移到△A′B′C′的位置,A′B′与⊙相切,作O′Q⊥A′B′于Q,
(2)如图2,△ABC从开始移动,到它的边与圆最后一次相切,即△ABC平移到△A′B′C′的位置,A′B′与⊙相切,作O′Q⊥A′B′于Q,则O′Q=1,
∴D′B′=1,
∵BD=5,DD′=t,BB′=2t,
∴5+t+1=2t,
∴t=6;
(3)
 当△ABC平移到△A1B1C1的位置,A1C1与⊙O相切,d=1,如图3,由(1)得C1D=
当△ABC平移到△A1B1C1的位置,A1C1与⊙O相切,d=1,如图3,由(1)得C1D=
| ||
| 3 |
∵BD=5,DD′=t,BB1=2t,
∴DB1=DD′-B1C1-C1D′=t-1-
| ||
| 3 |
∴5+t-1-
| ||
| 3 |
∴t=4-
| ||
| 3 |
当△ABC平移到△A2B2C2的位置,A2C2与⊙O相切,d=1,如图3,
作O′H⊥A2C2于H,
∵O′C2平分∠A2C2B2,
∴∠O′C2D′=30°,
∴C2D′=
| 3 |
| 3 |
∵CD+DD′+D′C2=CC2,
∴4+t+
| 3 |
∴t=4+
| 3 |
∴当d<1时,t的取值范围为4-
| ||
| 3 |
| 3 |
点评:本题考查了圆的综合题:掌握与圆有关的性质和切线的性质、直线与圆的位置关系;会利用含30度的直角三角形三边的关系进行计算;会应用一元一次方程解决几何计算问题.

练习册系列答案
相关题目
方程x2-2x=0的解为( )
| A、x1=0,x2=2 |
| B、x1=0,x2=-2 |
| C、x1=x2=1 |
| D、x=2 |
 如图,在?ABCD中,增加一个条件四边形ABCD就成为矩形,这个条件是( )
如图,在?ABCD中,增加一个条件四边形ABCD就成为矩形,这个条件是( )| A、AB=CD |
| B、∠A+∠C=180° |
| C、BD=2AB |
| D、AC⊥BD |