题目内容
 如图,已知△ABC中,AB=AC,∠B=2∠A,DE垂直平分AC交AB于点D,交AC于点E.求证:AD=BC.
如图,已知△ABC中,AB=AC,∠B=2∠A,DE垂直平分AC交AB于点D,交AC于点E.求证:AD=BC.考点:线段垂直平分线的性质,等腰三角形的性质
专题:证明题
分析:先根据△ABC中,AB=AC,∠B=2∠A求出∠A的度数,进而得出∠ACB与∠B的度数,再根据线段垂直平分线的性质得出AD=CD,故可得出∠A=∠ACD,再根据三角形外角的性质即可求出∠CDB的度数,进而得出结论.
解答:解:∵△ABC中,AB=AC,∠B=2∠A,
∴∠ACB=∠B=2∠A,
∴5∠A=180°,解得∠A=36°,
∴∠B=72°,
∵DE是线段AC的垂直平分线,
∴AD=CD,
∴∠A=∠ACD=36°,
∴∠CDB=∠A+∠ACD=72°,
∴∠CDB=∠B,
∴CD=BC,
∴AD=BC.
∴∠ACB=∠B=2∠A,
∴5∠A=180°,解得∠A=36°,
∴∠B=72°,
∵DE是线段AC的垂直平分线,
∴AD=CD,
∴∠A=∠ACD=36°,
∴∠CDB=∠A+∠ACD=72°,
∴∠CDB=∠B,
∴CD=BC,
∴AD=BC.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…求第10个正△A10B10C10的面积.
如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…求第10个正△A10B10C10的面积. 如图,某村有一口呈四边形的池塘,在它的四个角A,B,C,D处各栽有一棵大树.该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保留四棵大树,并要求扩建后的池成平行四边形,请问:村长能否实现这一设想?若能,请你帮村长设计并画出图形;若不能,请说明理由.
如图,某村有一口呈四边形的池塘,在它的四个角A,B,C,D处各栽有一棵大树.该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保留四棵大树,并要求扩建后的池成平行四边形,请问:村长能否实现这一设想?若能,请你帮村长设计并画出图形;若不能,请说明理由.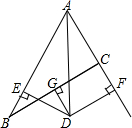 如图所示,在△ABC中,AB=8,AC=4,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC(或AC的延长线)于点D.
如图所示,在△ABC中,AB=8,AC=4,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC(或AC的延长线)于点D. 如图所示,在四边形ABCD中,O是AC和BD的交点,点E,F,G,H分别是AO,BO,CO,DO的中点,如果四边形EFGH是平行四边形,那么四边形ABCD也是平行四边形吗?说说你的理由.
如图所示,在四边形ABCD中,O是AC和BD的交点,点E,F,G,H分别是AO,BO,CO,DO的中点,如果四边形EFGH是平行四边形,那么四边形ABCD也是平行四边形吗?说说你的理由. 如图,M是?ABCD的边AB上任意一点,若△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S3,则S1,S2,S3的关系为
如图,M是?ABCD的边AB上任意一点,若△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S3,则S1,S2,S3的关系为