题目内容
12.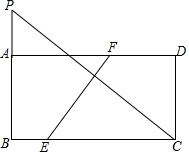 已知:如图,将矩形ABCD沿EF折叠,折痕交BC于点E,交AD于点F.若折叠后点C落在BA的延长线上P处,且AP=2,AB=4,AD=8,求折痕EF的长.
已知:如图,将矩形ABCD沿EF折叠,折痕交BC于点E,交AD于点F.若折叠后点C落在BA的延长线上P处,且AP=2,AB=4,AD=8,求折痕EF的长.
分析 作EH⊥AD于H,则EH=AB=4,在Rt△PBC中,BC=8,PB=PA+AB=6,利用勾股定理计算出PC=10,然后证明Rt△EFH∽Rt△CPB,再利用相似比可计算出EF.
解答 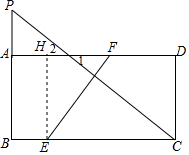 解:作EH⊥AD于H,如图2,
解:作EH⊥AD于H,如图2,
∴四边形ABEH为矩形,
∴EH=AB=4,
在Rt△PBC中,BC=8,PB=PA+AB=2+4=6,
∴PC=$\sqrt{P{B}^{2}+B{C}^{2}}$=10,
∵∠1+∠EFH=90°,∠P+∠2=90°,
而∠1=∠2,
∴∠EFH=∠P,
∴Rt△EFH∽Rt△CPB,
∴$\frac{EF}{PC}=\frac{EH}{BC}$,即$\frac{EF}{10}$=$\frac{4}{8}$,
∴EF=5.
点评 本题考查了折叠的性质:折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质、菱形的判定和相似三角形的判定与性质.

练习册系列答案
相关题目
2.为了解游客在野鸭湖国家湿地公园、松山自然保护区、玉渡山风景区和百里山水画廊这四个风景区旅游的满意率,数学小组的同学商议了几个收集数据的方案:
方案一:在多家旅游公司调查400名导游;
方案二:在野鸭湖国家湿地公园调查400名游客;
方案三:在玉渡山风景区调查400名游客;
方案四:在上述四个景区各调查100名游客.
在这四个收集数据的方案中,最合理的是( )
方案一:在多家旅游公司调查400名导游;
方案二:在野鸭湖国家湿地公园调查400名游客;
方案三:在玉渡山风景区调查400名游客;
方案四:在上述四个景区各调查100名游客.
在这四个收集数据的方案中,最合理的是( )
| A. | 方案一 | B. | 方案二 | C. | 方案三 | D. | 方案四 |
3.单项式-$\frac{2}{5}$a2b3的系数和次数分别是( )
| A. | -$\frac{2}{5}$,2 | B. | $\frac{2}{5}$,3 | C. | -$\frac{2}{5}$,5 | D. | $\frac{2}{5}$,6 |
7.在?ABCD中,AB=3cm,BC=6cm,一组对边之间的距离为4cm,则另一组对边之间的距离为( )
| A. | 8cm | B. | 8cm或2cm | C. | 2cm | D. | 无法确定 |

 一个几何体由几个大小相同的小正方形搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是4.
一个几何体由几个大小相同的小正方形搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是4.