题目内容
 如图,AB为圆O的直径,点C是圆O上一点,AC平分∠DAB,AD⊥CD,线段AB与DC的延长线交于点P.
如图,AB为圆O的直径,点C是圆O上一点,AC平分∠DAB,AD⊥CD,线段AB与DC的延长线交于点P.(1)求证:CD是圆O的切线;
(2)若PB=BO=1,求图中阴影部分的面积(结果保留根号).
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接OC,推出∠DAC=∠CAB,∠OAC=∠OCA,求出∠DAC=∠OCA,得出OC∥AD,推出OC⊥DC,根据切线的判定判断即可;
(2)连接OE、BC,证得△OBC是等边三角形,△OAE是等边三角形,进而求得△APD、△OAE、△OPC、弧形EOC的面积,用S△APD-S△OAE-S△OPC-S弧EOC即可求得图中阴影部分的面积;
(2)连接OE、BC,证得△OBC是等边三角形,△OAE是等边三角形,进而求得△APD、△OAE、△OPC、弧形EOC的面积,用S△APD-S△OAE-S△OPC-S弧EOC即可求得图中阴影部分的面积;
解答: 解:(1)连接OC,
解:(1)连接OC,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
又∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
又∵CD⊥AD,
∴OC⊥CD,
∴CD是圆O的切线.
(2)连接OE、BC,
∵PB=BO=1,
∴BC=OB=BP,
∵OB=OC,
∴OB=OC=BC,
∴△OBC是等边三角形,
∴∠OAD=60°,
∴△OAE是等边三角形,
∴∠EOC=60°,
∵AP=3OB=3,
∴AD=
AP=
,PD=
AP=
,
∴S△APD=
AD•PD=
×
×
=
,S△OAE=
×1×
=
,S△OPC=
OC•PC=
×1×
=
,S弧EOC=
=
,
∴阴影部分的面积=S△APD-S△OAE-S△OPC-S弧EOC=
-
-
-
=
-
;
 解:(1)连接OC,
解:(1)连接OC,∵AC平分∠DAB,
∴∠DAC=∠OAC,
又∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
又∵CD⊥AD,
∴OC⊥CD,
∴CD是圆O的切线.
(2)连接OE、BC,
∵PB=BO=1,
∴BC=OB=BP,
∵OB=OC,
∴OB=OC=BC,
∴△OBC是等边三角形,
∴∠OAD=60°,
∴△OAE是等边三角形,
∴∠EOC=60°,
∵AP=3OB=3,
∴AD=
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
9
| ||
| 8 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 60π•OC2 |
| 360 |
| π |
| 6 |
∴阴影部分的面积=S△APD-S△OAE-S△OPC-S弧EOC=
9
| ||
| 8 |
| ||
| 4 |
| ||
| 2 |
| π |
| 6 |
3
| ||
| 8 |
| π |
| 6 |
点评:此题考查了切线的判定,等边三角形的判定和性质,直角三角形的性质,直角三角函数的应用,三角形面积公式的应用,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
 如图已知△ABC,请你用直尺和圆规作图,作一个三角形,使它和△ABC全等.(要求用尺规作图,不必写你是如何作的,但是要保留作图时留下的作图痕迹)
如图已知△ABC,请你用直尺和圆规作图,作一个三角形,使它和△ABC全等.(要求用尺规作图,不必写你是如何作的,但是要保留作图时留下的作图痕迹)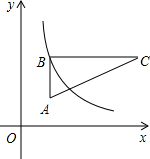 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4.