题目内容
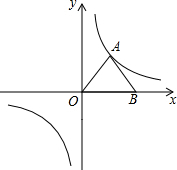如图，等边三角形AOB的边长为2，反比例函数
的图象经过点A，则k的值是
- A.
- B.
- C.2
- D.-2
A
分析：过点A作AD⊥x轴于点D，由锐角三角函数的定义求出A点坐标，再由反比例函数中k=xy的特点求出k的值即可．
解答：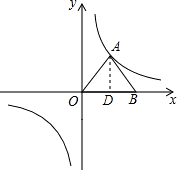
解：过点A作AD⊥x轴于点D，
∵等边三角形AOB的边长为2，
∴OD=
OB=×2=1，AD=OA×sin60°=2×
=，
∴A（1，），
∴k=1×=．
故选A．
点评：本题考查的是反比例函数图象上点的坐标特点及等边三角形的性质，熟知反比例函数y=
中k=xy的特点是解答此题的关键．
分析：过点A作AD⊥x轴于点D，由锐角三角函数的定义求出A点坐标，再由反比例函数中k=xy的特点求出k的值即可．
解答：
解：过点A作AD⊥x轴于点D，∵等边三角形AOB的边长为2，
∴OD=
OB=×2=1，AD=OA×sin60°=2×=，∴A（1，
），∴k=1×
=．故选A．
点评：本题考查的是反比例函数图象上点的坐标特点及等边三角形的性质，熟知反比例函数y=
中k=xy的特点是解答此题的关键． 
练习册系列答案
相关题目
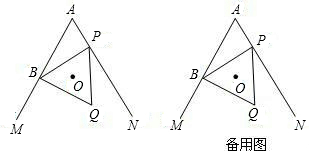
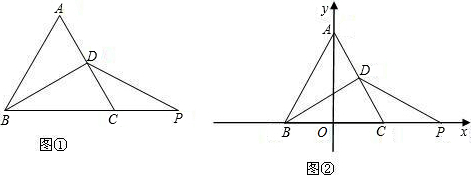
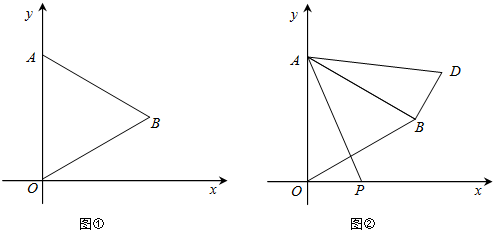
如图，等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO，分别交BC于点P，与⊙O交于点D，连接BD，CD．那么：①四边形BDCO是菱形，②若⊙O的半径为r，三角形的边长为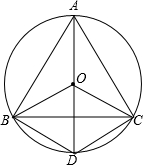
如图，等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO，分别交BC于点P，与⊙O交于点D，连接BD，CD．那么：