Question

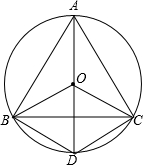如图，等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO，分别交BC于点P，与⊙O交于点D，连接BD，CD．那么：

①四边形BDCO是菱形，②若⊙O的半径为r，三角形的边长为r，

③三角形ODC是等边三角形，④弧BD的度数为60°，

其中正确的有

1. A.
   1个
2. B.
   2个
3. C.
   3个
4. D.
   4个

Answer 1

D
分析：证明△ABO≌△ACO，可得∠BAD=∠CAD=30°，从而可得BD=CD=AO，可判断①正确；在Rt△ABD中，根据BD=OB=r，∠BAD=30°，可求出AB，从而判断②正确；由①可得OC=OD=CD，从而判断③正确；求出∠BOD的度数，即可判断④正确；
解答：∵△ABC是等边三角形，
∴AB=AC=BC，
在△ABO和△ACO中，
∵，
∴△ABO≌△ACO（SSS），
∴∠BAD=∠CAD=30°，
则在Rt△ABD中，BD=AD=OB，
同理CD=AD=OB，
∵OB=OC=BD=CD，
∴四边形BDCO是菱形，故①正确；
在Rt△ABD中，AD=2r，BD=r，
∴AB==r，故②正确；
∵CO=OD=CD，
∴△ODC是等边三角形，故③正确；
∠BOD=2∠BAD=60°，
∴弧BD的度数为60°，故④正确．
综上可得：①②③④均正确，共4个．
故选D．
点评：本题考查了圆的综合，涉及了圆周角定理、等边三角形的性质、解直角三角形及全等三角形的判定与性质，综合性较强，解答本题的关键是掌握各知识点的内容，灵活运用．