题目内容
11.对于抛物线C:y=$\frac{1}{4m}$x2(m≠0,m为常数),存在点F(0,m)和直线y=-m,使抛物线C上的任意一点到点F和到直线y=-m的距离相等,我们把F叫做抛物线C的焦点,直线y=-m叫做抛物线C的准线.(1)如图1,抛物线C:y=$\frac{1}{4}$x2的焦点为F,准线为l,请直接写出F的坐标和准线l的解析式;
(2)在图1中,抛物线C的准线交y轴于点C,点A是抛物线C上任意一点,过A作AB⊥l于点B,连接FB交x轴于点E,连接CE.求证:CE2=FO•AB;
(3)如图2,将抛物线y=$\frac{1}{8}$x2沿x轴向右平移1个单位后,得到抛物线C1,此时抛物线C1的焦点为F1,准线为l1,点N的坐标为(5,5),点M是抛物线C1上的一动点,过点M作MK⊥l1于点K,连接MN,求|MN-MK|的最大值,并求出此时点M的坐标.
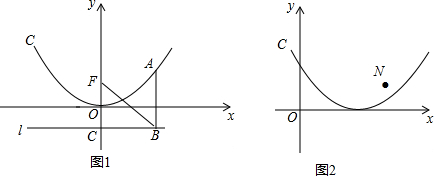
分析 (1)设F(0,b),A(t,$\frac{1}{4}$t2),则直线l的解析式为y=-b,根据两点间的距离公式,由AB=AF得到t2+($\frac{1}{4}$t2-b)2=($\frac{1}{4}$t2+b)2,解得b=1,于是得到点F的坐标为(0,1),准线l的解析式为y=-1;
(2)如图1,连结AF、AE,利用OF=OC可得CE=EF=EB,再由AF=AB,根据等腰三角形的性质得AE⊥BF,于是可证明Rt△ABE∽Rt△EFO,所以$\frac{AB}{EF}$=$\frac{BE}{OF}$,然后利用等线段代换即可得到结论;
(3)如图2,利用抛物线的平移变换得到抛物线C1的解析式为y=$\frac{1}{8}$(x-1)2,抛物线的对称轴为直线x=1,设F1(1,n),A[m,$\frac{1}{8}$(m-1)2],则l2的解析式为y=-n,根据两点间的距离公式由MK=MF1得到(m-1)2+[$\frac{1}{8}$(m-1)2-n]2=[$\frac{1}{8}$(m-1)2+n]2,解得n=2,则F1(1,2),接着利用待定系数法求出直线F1N的解析式为y=$\frac{3}{4}$x+$\frac{5}{4}$,由于|MN-MK|=|MN-MF1|,而当M、N、F1共线时,|MN-MK|最大,即M点为直线F1N与抛物线的交点式,|MN-MK|有最大值,然后通过解方程组$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{5}{4}}\\{y=\frac{1}{8}(x-1)^{2}}\end{array}\right.$即可得到M点的坐标.
解答 解: (1)设F(0,b),A(t,$\frac{1}{4}$t2),则直线l的解析式为y=-b,
(1)设F(0,b),A(t,$\frac{1}{4}$t2),则直线l的解析式为y=-b,
所以AB=$\frac{1}{4}$t2+b,
∵AB=AF,
∴t2+($\frac{1}{4}$t2-b)2=($\frac{1}{4}$t2+b)2,解得b=1,
∴点F的坐标为(0,1),准线l的解析式为y=-1;
(2)如图1,连结AF、AE,
∵OF=OC,
∴EF=EB,
∴CE=EF=EB,
而AF=AB,
∴AE⊥BF,
∴∠AEB=90°,
∵∠ABE=∠OFE,
∴Rt△ABE∽Rt△EFO,
∴$\frac{AB}{EF}$=$\frac{BE}{OF}$,即EF•BE=OF•AB,
∴CE2=OF•AB;
(3)如图2,抛物线C1的解析式为y=$\frac{1}{8}$(x-1)2,抛物线的对称轴为直线x=1,
设F1(1,n),A[m,$\frac{1}{8}$(m-1)2],则l2的解析式为y=-n,
∴MK=$\frac{1}{8}$(m-1)2+n,
∴MK=MF1,
∴(m-1)2+[$\frac{1}{8}$(m-1)2-n]2=[$\frac{1}{8}$(m-1)2+n]2,解得n=2,
∴F1(1,2),
设直线F1N的解析式为y=px+q,
把F1(1,2),N(5,5)代入得$\left\{\begin{array}{l}{p+q=2}\\{5p+q=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=\frac{3}{4}}\\{q=\frac{5}{4}}\end{array}\right.$,
∴直线F1N的解析式为y=$\frac{3}{4}$x+$\frac{5}{4}$,
∴|MN-MK|=|MN-MF1|,
∴当M、N、F1共线时,|MN-MK|最大,
解方程组$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{5}{4}}\\{y=\frac{1}{8}(x-1)^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=9}\\{y=8}\end{array}\right.$,
∴M点的坐标为(-1,$\frac{1}{2}$)或(9,8).
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质;能利用待定系数法求函数解析式和求抛物线与直线的交点坐标;理解坐标与图形的性质,记住两点间的距离公式;会运用相似比证明线段之间的关系;提高阅读理解能力.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案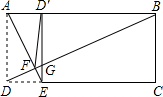 如图,在矩形ABCD中,AD=3.5,tan∠ABD=$\frac{2}{5}$,连接BD,E是CD上一点,连接AE,交BD于点F,将矩形ABCD沿AE折叠,点D恰好落在边AC的点D′处,则△EFD′的面积为( )
如图,在矩形ABCD中,AD=3.5,tan∠ABD=$\frac{2}{5}$,连接BD,E是CD上一点,连接AE,交BD于点F,将矩形ABCD沿AE折叠,点D恰好落在边AC的点D′处,则△EFD′的面积为( )| A. | 1.75 | B. | 3 | C. | 3.5 | D. | 4 |
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
| A. | $\frac{{{x^2}+x}}{{{x^2}+2}}=\frac{x}{2}$ | B. | $\frac{{{x^2}-2x}}{2y-xy}=\frac{x}{y}$ | ||
| C. | $\frac{{{x^2}-9}}{{{x^2}-6x+9}}=\frac{x+3}{x-3}$ | D. | $\frac{x+2}{{{x^2}+4}}=\frac{1}{x+2}$ |
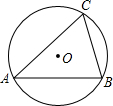 如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.
如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.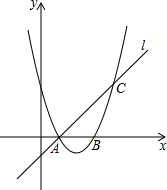 如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点的坐标是(4,3).
如图,已知抛物线y=ax2+bx+3与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点的坐标是(4,3). 已知如图,△ABC为等边三角形,边长为a,点F是BC上任意一点,DF⊥AB,EF⊥AC
已知如图,△ABC为等边三角形,边长为a,点F是BC上任意一点,DF⊥AB,EF⊥AC