题目内容
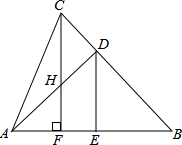 如图,已知在△ABC中,BA=BC,∠B=45°,将△ABC折叠,使点B与点A重合,折痕为DE,CF⊥AB于F,交AD于H,求证:△AFH≌△CDH.
如图,已知在△ABC中,BA=BC,∠B=45°,将△ABC折叠,使点B与点A重合,折痕为DE,CF⊥AB于F,交AD于H,求证:△AFH≌△CDH.考点:全等三角形的判定与性质
专题:证明题
分析:根据折叠求出∠DAB=∠B=45°,求出∠ADB=90°,求出∠BCF=∠BAD,根据等腰三角形的性质求出∠BCA=∠BAC,求出∠HCA=∠HAC,推出CH=AH,根据AAS推出两三角形全等即可.
解答:证明:∵将△ABC折叠,使点B与点A重合,折痕为DE,
∴AD=BD,
∵∠B=45°,
∴∠DAB=∠B=45°,
∴∠ADB=90°,
∵CF⊥AB,
∴∠CFA=∠CFB=90°,∠BCF=90°-45°=45°,
∴∠DAB=∠BCF,
∵AB=BC,
∴∠BCA=∠BAC,
∴∠BCA-∠BCF=∠BAC-∠DAB,
∴∠FCA=∠DAC,
∴CH=AH,
在△AFH和△CDH中,
,
∴△AFH≌△CDH(AAS).
∴AD=BD,
∵∠B=45°,
∴∠DAB=∠B=45°,
∴∠ADB=90°,
∵CF⊥AB,
∴∠CFA=∠CFB=90°,∠BCF=90°-45°=45°,
∴∠DAB=∠BCF,
∵AB=BC,
∴∠BCA=∠BAC,
∴∠BCA-∠BCF=∠BAC-∠DAB,
∴∠FCA=∠DAC,
∴CH=AH,
在△AFH和△CDH中,
|
∴△AFH≌△CDH(AAS).
点评:本题考查了全等三角形的判定,三角形内角和定理,等腰三角形的性质和判定的应用,解此题的关键是求出全等的三个条件,题目比较好,难度适中.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
长方形的一边等于2a+3b,另一边比它大a-b,则此长方形的周长为( )
| A、10a+10b |
| B、6a+4b |
| C、4a+6b |
| D、3a+2b |
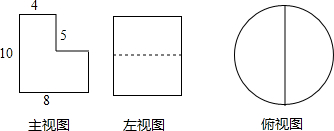 一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积.
一个几何体的三视图如图所示,你能画出这个几何体吗?并求出它的表面积和体积.