题目内容
抛物线y=x2-4x-3的顶点坐标为 ．
考点：二次函数的性质
专题：
分析：已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点，直接写出顶点坐标．
解答：解：y=x2-4x-3=y=x2-4x+4-4-3=（x-2）2-7，
顶点坐标为（2，-7），
故答案为：（2，-7）．
顶点坐标为（2，-7），
故答案为：（2，-7）．
点评：此题考查了二次函数的性质，二次函数y=a（x-h）2+k的顶点坐标为（h，k），对称轴为x=h，此题还考查了配方法求顶点式．
练习册系列答案
相关题目
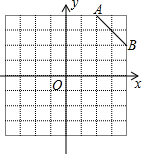如图在8×8的正方形网格中建立直角坐标系，已 知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形，画出图形，并解答下列问题：
如图，已知AP平分∠BAC，DP平分∠CDB，∠C=50°，∠B=20°，则∠P的度数为（ ）| A、10° | B、15° |
| C、30° | D、40° |
使分式
有意义的x的取值范围是（ ）
| 2 |
| x-3 |
| A、x≤3 | B、x≥3 |
| C、x≠3 | D、x=3 |