题目内容
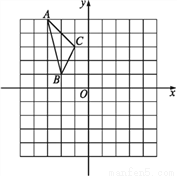
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
练习册系列答案
相关题目
根据关于x的一元二次方程x2+px+q=0,可列表如下:则方程x2+px+q=0的正数解满足( )
x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
x2+px+q | ﹣15 | ﹣8.75 | ﹣2 | ﹣0.59 | 0.84 | 2.29 |
A. 解的整数部分是0,十分位是5 B. 解的整数部分是0,十分位是8
C. 解的整数部分是1,十分位是1 D. 解的整数部分是1,十分位是2
C 【解析】根据表中函数的增减性,可以确定函数值是0时,x应该是大于1.1而小于1.2. 所以解的整数部分是1,十分位是1. 故选:C.

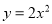 先向右平移1个单位,再向下平移3个单位得到的抛物线解析式为( )
先向右平移1个单位,再向下平移3个单位得到的抛物线解析式为( )