题目内容
4.(1)计算:|1-$\sqrt{3}$|+3tan30°-($\sqrt{3}-5$)0-(-$\frac{1}{3}$)-1.(2)解不等式组$\left\{\begin{array}{l}{2x+1>0①}\\{\frac{2-x}{2}≥\frac{x+3}{3}②}\end{array}\right.$.
分析 (1)首先去掉绝对值符号,计算乘方,代入特殊角的三角函数值,然后进行加减计算即可;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)原式=$\sqrt{3}$-1+3×$\frac{\sqrt{3}}{3}$-1-(-3)=$\sqrt{3}$-1+$\sqrt{3}$-1+3=2$\sqrt{3}$+1;
(2)解①得x>-$\frac{1}{2}$,
解②得x≤0,
则不等式组的解集是-$\frac{1}{2}$<x≤0.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
15.面积为2的正方形的边长在( )
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
19.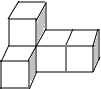 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
 由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )
由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )| A. | 主视图的面积最小 | B. | 左视图的面积最小 | ||
| C. | 俯视图的面积最小 | D. | 三个视图的面积相等 |
9.下列计算正确的是( )
| A. | x2+3x2=4x4 | B. | x2y•2x3=2x4y | C. | (6x3y2)÷(3x)=2x2 | D. | (-3x)2=9x2 |
 如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE. 如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.
如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2. 如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( ) 如图,点A、B、C、D在⊙O上,且四边形OABC为菱形,则∠ADC=60°.
如图,点A、B、C、D在⊙O上,且四边形OABC为菱形,则∠ADC=60°.