题目内容
6.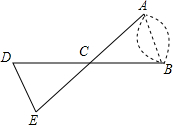 如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.
如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.(1)测量方案:
(2)理由:
分析 (1)先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至E,BC至D,使EC=AC,DC=BC,最后测出DE的距离即为AB的长;
(2)利用SAS证明△EDC≌△ABC,根据全等三角形的对应边相等得到ED=AB.
解答 解:(1)测量方案:先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至E,BC至D,使EC=AC,DC=BC,最后测出DE的距离即为AB的长;
(2)理由:
在△EDC和△ABC中,
$\left\{\begin{array}{l}{EC=AC}\\{∠DCE=∠BCA}\\{DC=BC}\end{array}\right.$,
∴△EDC≌△ABC(SAS),
∴ED=AB(全等三角形对应边相等),
即DE的距离即为AB的长.
点评 本题考查了全等三角形的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
16.某商品降低x%后是a元,则原价是( )
| A. | a•x%元 | B. | a(1+x%)元 | C. | $\frac{a}{x%}$元 | D. | $\frac{a}{1-x%}$元 |
17.将边长为1的正方形纸片如图1所示的方法进行对折,记第一次对折后得到的图形面积为 S1,第2次对折后得到的图形面积为S2…,第n次对折后得到的图形面积为Sn,请根据图2化简S1+S2+S3…S2014=( )
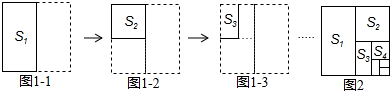

| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
14.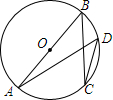 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
8. 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )| A. | 3.40×102 | B. | 340×104 | C. | 3.40×104 | D. | 3.40×106 |
 如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.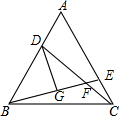 已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证: 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.