题目内容
如图，已知AB、CD是⊙O的直径，弦CF∥AP，BF、PD相交于E，求证：OE∥PA．考点：圆周角定理,圆心角、弧、弦的关系
专题：证明题
分析：由CF∥AP可得
=
，则
=
，进而利用O、E、B、D四点共圆，得出∠BOE=∠BDE=∠BAP进而得出答案．
 |
| PF |
|
| AC |
|
| PC |
|
| AF |
解答：
证明：∵CF∥AP，
∴
=
，则
=
，
∴∠CDP=∠ABF，
连接BD，
则O、E、B、D四点共圆，
∴∠BOE=∠BDE=∠BAP，
∴OE∥PA．
证明：∵CF∥AP，∴
|
| PF |
|
| AC |
|
| PC |
|
| AF |
∴∠CDP=∠ABF，
连接BD，
则O、E、B、D四点共圆，
∴∠BOE=∠BDE=∠BAP，
∴OE∥PA．
点评：此题主要考查了圆周角定理以及四点共圆，得出O、E、B、D四点共圆是解题关键．
练习册系列答案
相关题目
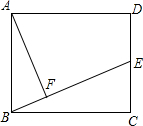在矩形ABCD中，AB=10，BC=12，E为CD的中点，连接B、E，作AF⊥BE，垂足为F，则AF=
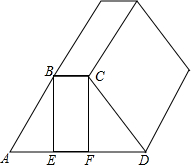梯形ABCD是一段公路路基的截面图，现在需要在2个斜坡面植草，已知∠A=45°，DE=8m，DF=6m，路基长30m，每平方米的草坪的费用为a元，求2个斜坡面植草的总费用．
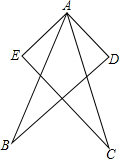如图，AD=AE，∠EAB=∠DAC，∠B=∠C．求证：AB=AC．