Question

19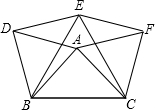．如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、△BCE、△ACF，请回答下列问题，并说明理由．
（1）求证：四边形ADEF是平行四边形；
（2）若∠BAC=90°，AB=4，AC=6，求四边形ADEF的面积．
（3）当△ABC满足什么条件时，以A，D，E，F为顶点的四边形不存在，请说明理由．

Answer 1

分析 （1）利用三角形全等，只要证明DE=AF，AD=EF即可解决问题．
（2）作AH⊥DE于H，先证明∠ADF=30°，求出AH即可解决问题．
（3）当∠BAC=60°时，∠DAF=180°，此时D、A、F三点在同一条直线上，以A，D，E，F为顶点的四边形就不存在．

解答 解：（1）四边形ADEF是平行四边形．
理由：∵△ABD，△EBC都是等边三角形．
∴AD=BD=AB，BC=BE=EC
∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA．
∴∠DBE=∠ABC．
在△DBE和△ABC中，
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABC}\\{BE=BC}\end{array}\right.$，
∴△DBE≌△ABC．
∴DE=AC．
又∵△ACF是等边三角形，
∴AC=AF．
∴DE=AF．
同理可证：AD=EF，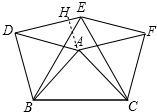
∴四边形ADEF是平行四边形．

（2）作AH⊥DE于H．
∵四边形ADEF是平行四边形，
∴DE∥AF，DE=AF=AC=6，AD=EF=AB=4，
∴∠ADE+∠DAF=180°，
∵∠DAF=360°-60°-60°-90°=150°，
∴∠ADE=30°
∴AH=$\frac{1}{2}$AD=2，
∴S_{平行四边形ADEF}=DE•AH=12．
（3）当∠BAC=60°时，以A，D，E，F为顶点的四边形不存在．
理由：∵∠BAC=60°，
∴∠ADF=360°-∠DAB-∠BAC-∠CAF=360°-60°-60°-60°=180°，
∴D、A、F三点共线，
∴以A，D，E，F为顶点的四边形不存在．

点评 本题考查等边三角形的性质，全等三角形的性质与判定、平行四边形面积等知识，解题的关键是正确寻找全等三角形，学会添加常用辅助线，属于中考常考题型．