Question

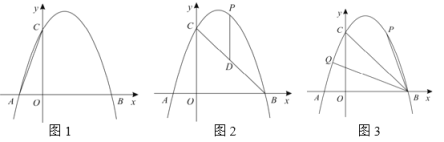
【题目】如图1，抛物线过点轴上的和点，交轴于点，点该物上限一点，且．

（1）抛物线的解析式为：____________；

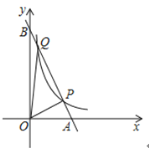
（2）如图2，过点作轴交直线于点，求点在运动的过程中线段长度的最大值；

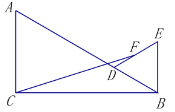
（3）如图3，若，在对称轴左侧的抛物线上是否存在点，使？若存在，请求出点的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）；（2）；（3）存在，

【解析】

（1）根据，易知点C(0,3),将点A，C的坐标代入中，即可得到b，c的值，从而得到抛物线的解析式；

（2）先根据B,C坐标确定直线BC的解析式为，设,则，则PD的长度为，结合x的取值范围，利用二次函数的性质求PD长度的最大值；

（3）首先由，OB=OC,易知∠BCP=∠OCB=45° ，得到PC//OB,设直线BQ与y轴交于点G,结合条件证得△CPB≌△CGB，得到CG=CP=2，得到点G的坐标，利用B，G得到直线BQ的解析式，再与抛物线的解析式联立方程组，从而求得交点Q的坐标并说明了其存在.

解：（1）∵，易知点C(0,3), 将点A，C的坐标代入中得到 ，解得，∴抛物线的解析式为：.

（2）由，得B（3，0）

设直线BC的解析式为

将点代入得

∴直线BC的解析式为

设点，则

∴

.

∴当时，PD有最大值.

（3）存在

∵，点P在第一象限，∴

∵B（3，0），C（0，3）

∴OC=OB

∴△BOC是等腰直角三角形

∴∠OBC=∠OCB=45°

∴∠BCP=∠OCB=45°，∴CP∥OB，∴P（2，3）

设BQ与y轴交于点G

在△CPB和△CGB中：

，∴△CPB≌△CGB（ASA）

∴CG=CP=2

∴OG=1

∴点G（0，1），

设直线BQ：

将点B（3，0）代入，∴，

∴直线BQ：，

联立直线BQ和二次函数解析式

解得：或（舍去）

.