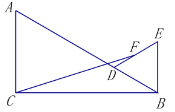
题目内容
【题目】如图，
中，
，
，
，
是线段
上一个动点，以
为边在
外作等边
．若
是
的中点，则
的最小值为（ ）
A.6B.8C.9D.10
【答案】C
【解析】
过点D作DG⊥BC于G，过点F作FH⊥BC于H，设等边△BDE的边长为x，解直角三角形BG，DG，再求出∠CBE=90°，然后根据梯形的中位线等于两底和的一半求出FH，再求出CH，然后利用勾股定理列式表示出CF2，再根据二次函数的增减性求出CF2的最小值，然后开方即可．
解：如图，过点D作DG⊥BC于G，过点F作FH⊥BC于H，
设等边△BDE的边长为x，
∵∠ABC=30°，
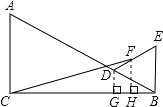
∴BG=
x，DG=
x，
∵∠ABC=30°，△BDE是等边三角形，
∴∠CBE=90°，
∵F为DE中点，
∴FH是梯形BEDG的中位线，
在
中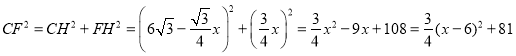
为线段AB上一个动点
当
时 
有最小值81
:CF的最小值为
，
故选择：C
练习册系列答案
相关题目
【题目】某生产商存有1200千克
产品，生产成本为150元/千克，售价为400元千克.因市场变化，准备低价一次性处理掉部分存货，所得货款全部用来生产
产品，产品售价为200元/千克.经市场调研发现，产品存货的处理价格
（元/千克）与处理数量
（千克）满足一次函数关系（
），且得到表中数据.
|
|
200 | 350 |
400 | 300 |
（1）请求出处理价格（元千克）与处理数量（千克）之间的函数关系；
（2）若产品生产成本为100元千克，产品处理数量为多少千克时，生产产品数量最多，最多是多少？
（3）由于改进技术，产品的生产成本降低到了
元/千克，设全部产品全部售出，所得总利润为
（元），若
时，满足随的增大而减小，求的取值范围.
