题目内容
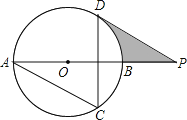
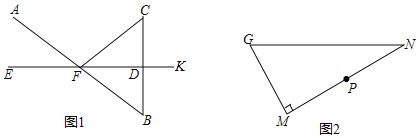
【题目】如图①,在△ABC中,以AB为直径的⊙O交AC于点D,点E在BC上,连接BD,DE,∠CDE=∠ABD.
(1)求证:DE是⊙O的切线.
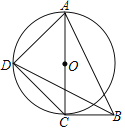
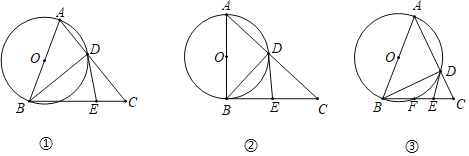
(2)如图②,当∠ABC=90°时,线段DE与BC有什么数量关系?请说明理由.
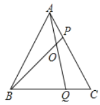
(3)如图③,若AB=AC=10,sin∠CDE=![]() ,求BC的长.
,求BC的长.
【答案】(1)见解析;(2)DE=![]() BC,见解析;(3)4
BC,见解析;(3)4![]()
【解析】
(1)先判断出∠BDC=90°,再判断出∠ABD=∠ODB,即可得出结论;
(2)先判断出BE=DE,再判断出CE=DE,即可得出结论;
(3)先利用三角函数求出AB=10,AD=6,再用勾股定理求出BD=8,即可得出结论.
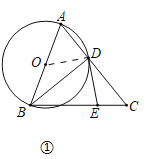
解:(1)证明:如图①,连接OD.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠CDE+∠BDE=∠BDC=90°.
∵∠CDE=∠ABD,
∴∠ABD+∠BDE=90°.
∵OB=OD,
∴∠ABD=∠ODB,
∴∠ODB+∠BDE=90°,
即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)DE=![]() BC.
BC.
理由如下:由(1)知∠ODE=90°,
∴∠ODB+∠BDE=90°.
∵∠ABC=90°,
∴∠OBD+∠DBE=90°.
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DBE=∠BDE,
∴BE=DE.
∵∠ABC=90°,
∴∠C+∠A=90°.
∵∠ABD+∠A=90°,
∴∠C=∠ABD.
∵∠CDE=∠ABD,
∴∠C=∠CDE,
∴DE=CE,
∴BE=DE=CE.
∴DE=![]() BC.
BC.
(3)∵∠CDE=∠ABD,
∴sin∠CDE=sin∠ABD=![]() .
.
在Rt△ABD中,
∵sin∠ABD=![]() =
=![]() ,AB=10,
,AB=10,
∴AD=![]() AB=
AB=![]() ×10=6,
×10=6,
∴BD=![]() =
=![]() =8.
=8.
在Rt△BDC中,∠BDC=90°,CD=10﹣6=4,
∴BC=![]() =
=![]() =4
=4![]() .
.

 考前必练系列答案
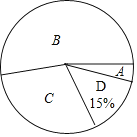
考前必练系列答案【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数,并对数据进行整理、描述和分析。
下面给出了部分信息:(说明:45 个以下为产量不合格,45 个及以上为产量合格,其中 45~65 个为产量良好,65~85 个为产量优秀)
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85):
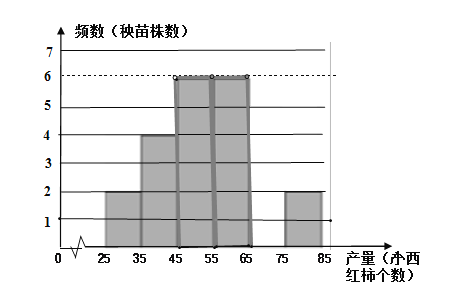
b.乙组数据在产量良好(45≤x<65)这两组的具体数据为: 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
(1)补全乙的频数分布直方图.
(2)写出表中![]() 的值.
的值.
(3)根据样本情况,估计乙大棚产量良好及以上的秧苗数为 株.
(4)根据抽样调查情况,可以推断出 大棚的小西红柿秧苗品种更适应市场需求,写出理由.(至少从两个不同的角度说明推断的合理性).