题目内容
11.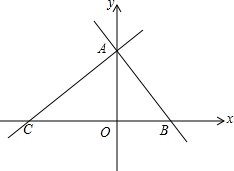 如图,在平面直角坐标系中,直线AC与x轴交于C点,与y轴交于A点,直线AB与x轴交于B点,与y轴交于A点,已知A(0,4),B(2,0).
如图,在平面直角坐标系中,直线AC与x轴交于C点,与y轴交于A点,直线AB与x轴交于B点,与y轴交于A点,已知A(0,4),B(2,0).(1)求直线AB的解析式.
(2)若S△ABC=7,求点C的坐标.
分析 (1)设直线AB的解析式为y=kx+b,把A(0,4),B(2,0)代入即可得出答案;
(2)根据S△ABC=7得出BC的长度,从而得出点C的坐标.
解答 解:(1)设直线AB的解析式为y=kx+b
∵直线AB经过A(0,4),B(2,0)
∴$\left\{\begin{array}{l}{b=4}\\{2k-b=0}\end{array}\right.$,
解之得$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=-2x+4;
(2)设C(x,0)
∵A(0,4),B(2,0)
∴OA=4,OB=2
∵S△ABC=7,
∴$\frac{1}{2}$BC•OA=7,
∴BC=3.5,
∴|x-2|=3.5,
解得:x=5.5或x=-1.5,
∴C(-1.5,0)或C(5.5,0).
点评 本题考查了两条直线相交或平行问题,以及一次函数的性质,熟知用待定系数法求一次函数的解析式是解答此题的关键.

练习册系列答案
相关题目
2.经统计2012年某市中考考生人数达56940人,数据56940用科学记数法可以表示为(要求保留三位有效数字)( )
| A. | 56.950×103 | B. | 5.6950×104 | C. | 5.70×104 | D. | 5.69×104 |
16.据统计,2013年长春市第十届汽博会展会观众累计约690000人次.将690000这个数用科学记数法表示为( )
| A. | 69×104 | B. | 7×106 | C. | 6.9×106 | D. | 6.9×105 |
 如图,在平面直角坐标系中,菱形OABC的顶点A在y轴正半轴上,顶点B在第二象限,∠C=60°,函数y=$\frac{k}{x}$(k<0,x<0)的图象经过点B.若菱形OABC的面积为2$\sqrt{3}$,则k的值为-$\sqrt{3}$.
如图,在平面直角坐标系中,菱形OABC的顶点A在y轴正半轴上,顶点B在第二象限,∠C=60°,函数y=$\frac{k}{x}$(k<0,x<0)的图象经过点B.若菱形OABC的面积为2$\sqrt{3}$,则k的值为-$\sqrt{3}$. 如图,若DE∥BC,AD=3cm,DB=2cm,则$\frac{DE}{BC}$=3:5.
如图,若DE∥BC,AD=3cm,DB=2cm,则$\frac{DE}{BC}$=3:5.