题目内容
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D.
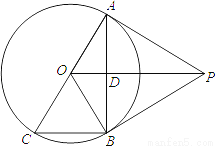
(1)求证:PB是⊙O的切线.
(2)当BC=2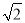 ,cos∠AOD=
,cos∠AOD=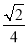 时,求PB的长.
时,求PB的长.
练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D.

(1)求证:PB是⊙O的切线.
(2)当BC=2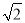 ,cos∠AOD=
,cos∠AOD=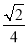 时,求PB的长.
时,求PB的长.
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案