题目内容
19.若点A(x1,y1),B(x2,y2)在反比例函数y=$\frac{k-3}{x}$(x>0)图象上,当x1<x2时,y1<y2,则k的取值范围是( )| A. | k<3 | B. | k≤3 | C. | k>3 | D. | k≥3 |
分析 根据反比例函数的性质由0<x1<x2时,y1<y2得到k-3<0,然后解不等式即可.
解答 解:∵当0<x1<x2时,y1<y2,
∴反比例函数图象在第四象限,
∴k-3<0,
∴k<3.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.

练习册系列答案
相关题目
14.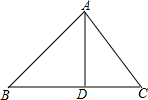 如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )
如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )
 如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )
如图,AB⊥AC,AD⊥BC,如果AB=4cm,AC=3cm,AD=2.4cm,那么点C到直线AB的距离为( )| A. | 3cm | B. | 4cm | C. | 2.4cm | D. | 无法确定 |
8.下列各式中,与(2-$\sqrt{3}$)的积为有理数的是( )
| A. | 2$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
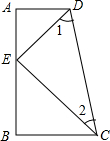 如图,CB⊥AB于点B,DA⊥AB于点A,CE平分∠BCD,DE平分∠CDA,点E在AB上,请问:∠1和∠2有何等量关系?并证明你的结论.
如图,CB⊥AB于点B,DA⊥AB于点A,CE平分∠BCD,DE平分∠CDA,点E在AB上,请问:∠1和∠2有何等量关系?并证明你的结论.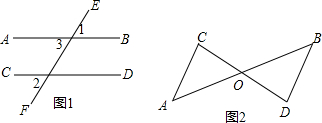 根据下列证明过程填空:
根据下列证明过程填空: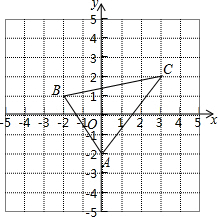 如图、已知A(0、-2)、B(-2、1)、C(3、2)
如图、已知A(0、-2)、B(-2、1)、C(3、2) 已知:如图,点B,E,C,F在一条直线上,AB∥DE,∠A=∠D,AC⊥BF,AC与DE相交于点M,对DF⊥BF说明理由.
已知:如图,点B,E,C,F在一条直线上,AB∥DE,∠A=∠D,AC⊥BF,AC与DE相交于点M,对DF⊥BF说明理由.