题目内容
14．用黑白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案：
第（6）个图案中有白色地砖26块，那么第（n）个图案中有白色地砖4n+2块．
分析 设第（n）个图形中有白色地砖an块，根据给定图形中白色地砖数目的变化找出变化规律“an=4n+2”，依次规律即可得出结论．
解答 解：设第（n）个图形中有白色地砖an块，
观察，发现规律：a1=6=4×1+2，a2=10=4×2+2，a3=14=4×3+2，…，
∴an=4n+2．
当n=6时，a6=4×6+2=26．
故答案为：26；4n+2．
点评 本题考查了规律型中图形的变化类，根据图形中白色地砖数目的变化找出变化规律an=4n+2是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠B=∠C，∠BAD=34°，且∠ADE=∠AED，则∠CDE=17度．
5．
如图，平行四边形ABOC中，对角线AO与BC相交于点E，双曲线y=$\frac{k}{x}$（k＜0）经过C，E两点，若平行四边形ABOC的面积为36，则k的值是（ ）
如图，平行四边形ABOC中，对角线AO与BC相交于点E，双曲线y=$\frac{k}{x}$（k＜0）经过C，E两点，若平行四边形ABOC的面积为36，则k的值是（ ）| A． | -$\frac{5}{2}$ | B． | -$\frac{10}{3}$ | C． | -4 | D． | -5 |
2．为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果做了民意调查，那么最终买什么水果，下面的调查数据中最值得关注的是（ ）
| A． | 众数 | B． | 平均数 | C． | 中位数 | D． | 方差 |
19．
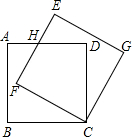如图，边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，则四边形DHFC的面积为（ ）
如图，边长为$\sqrt{3}$的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，则四边形DHFC的面积为（ ）| A． | $\sqrt{3}$ | B． | 3$\sqrt{3}$ | C． | 9 | D． | 6$\sqrt{3}$ |
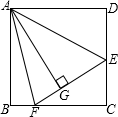如图，在正方形ABCD中，AB=BC=CD=AD，∠BAD=∠B=∠C=∠D=90°，点E、F分别在正方形ABCD的边DC、BC上，AG⊥EF且 AG=AB，垂足为G，则：