题目内容
二次函数y=x2-2x-2与坐标轴的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:抛物线与x轴的交点
专题:
分析:先计算根的判别式的值,然后根据b2-4ac决定抛物线与x轴的交点个数进行判断.
解答:解:∵△=(-2)2-4×1×(-2)=12>0,
∴二次函数y=x2-2x-2与x轴有2个交点,与y轴有一个交点.
∴二次函数y=x2-2x-2与坐标轴的交点个数是3个.
故选D.
∴二次函数y=x2-2x-2与x轴有2个交点,与y轴有一个交点.
∴二次函数y=x2-2x-2与坐标轴的交点个数是3个.
故选D.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系:△=b2-4ac决定抛物线与x轴的交点个数;△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如果a=b,那么下列结论中不一定成立的是( )
A、
| ||
| B、a-b=0 | ||
| C、2a=a+b | ||
| D、a2=ab |
 如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )
如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )| A、落在菱形内 | B、落在圆内 |
| C、无法判断 | D、一样大 |
下列各式中,正确的是( )
| A、(-1)99=-99 |
| B、-(-22)=4 |
| C、-102=(-10)×(-10) |
| D、2-|-2|=4 |
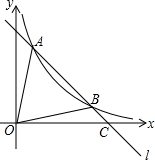 如图,直线l与反比例函数y=
如图,直线l与反比例函数y=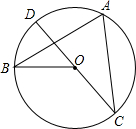 如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是
如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是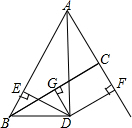 如图,AB>AC,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,∠BDE=∠CDF,BE=3,AC=6,求AE的长.
如图,AB>AC,∠BAC的平分线与BC的垂直平分线交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,∠BDE=∠CDF,BE=3,AC=6,求AE的长. 如图,已知AC和BD相交于点 O,∠AOB=∠A,∠COD=∠C.问∠A和∠C之间有什么大小关系?请说明理由.
如图,已知AC和BD相交于点 O,∠AOB=∠A,∠COD=∠C.问∠A和∠C之间有什么大小关系?请说明理由. 如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点
如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点