题目内容
7.m为何值时,2(m+1)x2+4mx+(3m-2)=0有实数根?分析 根据方程为一元一次方程和一元二次方程两种情况分类讨论,根据根的判别式得出m的范围即可.
解答 解:当2(m+1)=0,即m=-1时,原方程为-4x-5=0,此时方程的解为x=-$\frac{5}{4}$,
当2(m+1)≠0,即m≠-1时,根据题意,得:(4m)2-8(m+1)(3m-2)≥0,
即m2+m-2≤0,
解得:-2≤m≤1,
综上,-2≤m≤1.
点评 本题主要考查一元二次方程根的判别式和一元二次方程的定义,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
15.市场上猪肉的价格是9.6元/斤,很不好计算金额,但某销售员总能脱口说出金额,原来他记住了下列的表格:
(1)此题中的两个变量分别是x和y,其中自变量是x,因变量是y,y是x的函数.
(2)这是用哪种方法表示的函数?
(3)你能写出y与x之间的关系式吗?
| 斤数x | 1.1 | 1.2 | 1.3 | 1.4 |
| 金额y | 10.56 | 11.52 | 12.48 | 13.44 |
(2)这是用哪种方法表示的函数?
(3)你能写出y与x之间的关系式吗?
20.有四条线段,分别为3,4,5,6,从中任取三条,能够成直角三角形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
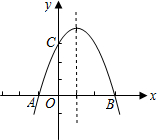 如图所示的抛物线是由抛物线y=-x2向上平移4个单位长度,再向右平移1个单位长度得到,与y轴交于C点.
如图所示的抛物线是由抛物线y=-x2向上平移4个单位长度,再向右平移1个单位长度得到,与y轴交于C点. 如图是一个数值转换器,若输入的值为3,则输出的值是65.
如图是一个数值转换器,若输入的值为3,则输出的值是65. 画出旋转后的图形:如图,将点线段AB绕点O旋转,使A点的对应点为点A′.
画出旋转后的图形:如图,将点线段AB绕点O旋转,使A点的对应点为点A′.