题目内容
20.阅读理解.∵$\sqrt{4}$<$\sqrt{5}$<$\sqrt{9}$,即2<$\sqrt{5}$<3.
∴1<$\sqrt{5}$-1<2
∴$\sqrt{5}$-1的整数部分为1,
∴$\sqrt{5}$-1的小数部分为$\sqrt{5}$-2.
解决问题:已知a是$\sqrt{17}$-3的整数部分,b是$\sqrt{17}$-3的小数部分.
(1)求a,b的值;
(2)求(-a)3+(b+4)2的平方根,提示:($\sqrt{17}$)2=17.
分析 (1)根据被开饭数越大算术平方根越大,可得a,b的值,
(2)根据开平方运算,可得平方根.
解答 解:(1)∴$\sqrt{16}$<$\sqrt{17}$<$\sqrt{25}$,
∴4$<\sqrt{17}$<5,
∴1<$\sqrt{17}$-3<2,
∴a=1,b=$\sqrt{17}$-4;
(2)(-a)3+(b+4)2=(-1)3+($\sqrt{17}$-4+4)2=-1+17=16,
∴(-a)3+(b+4)2的平方根是±$\sqrt{16}$=±4.
点评 本题考查了估算无理数的大小,利用被开饭数越大算术平方根越大得出4$<\sqrt{17}$<5是解题关键.

练习册系列答案
相关题目
8.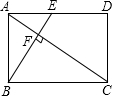 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
12.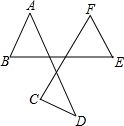 如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
 如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
10.圆柱的侧面展开图是正方形,则底面直径与高的比是( )
| A. | 1:2π | B. | π:2 | C. | 1:π | D. | 1:1 |
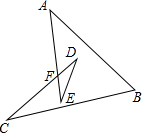 如图,求∠A+∠B+∠C+∠D+∠E的度数:180°.
如图,求∠A+∠B+∠C+∠D+∠E的度数:180°.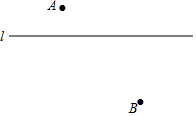 尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B. (1)如图:A、B、C、D四点在同一直线上,若AB=CD.
(1)如图:A、B、C、D四点在同一直线上,若AB=CD.