题目内容
1.抛物线y=ax2+(a-3)x-a-1经过原点,那么a的值等于( )| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
分析 把原点坐标代入函数解析式计算,再根据二次项系数不等于0解答
解答 解:∵抛物线y=ax2+(a-3)x-a-1经过原点,
∴-a-1=0,
解得a=-1,
故选C.
点评 本题考查了函数图象上点的坐标特征,二次函数的性质,熟记性质是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
12.下列平面图形经过折叠不能围成棱柱的是( )
| A. |  | B. |  | C. |  | D. |  |
9.若$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$是方程x-ky=0的解,则k的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
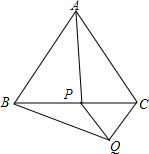 (1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.
(1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.