如图.在△ABC中.∠B.∠C的平分线交于点D．过点D作EF∥BC.与AB交于点E.与AC交于点F．已知AB=6cm.AC=4cm.求△AEF的周长．题目和参考答案——青夏教育精英家教网—

题目内容

5．

如图，在△ABC中，∠B、∠C的平分线交于点D．过点D作EF∥BC，与AB交于点E，与AC交于点F．已知AB=6cm，AC=4cm，求△AEF的周长．

分析由平行和角平分线可得∠EDB=∠EBD，可得ED=EB，同理可得出FD=FC，则有AE+EF+AF=AE+ED+DF+AF=AB+AC，可求得△AEF的周长．

解答解：∵EF∥BC，
∴∠EDB=∠DBC，
∵BD平分∠ABC，
∴∠EBD=∠DBC，
∴∠EBD=∠EDB，
∴EB=ED，
同理可得FD=FC，
∴AE+EF+AF=AE+ED+DF+AF=AE+EB+FC+AF=AB+AC=6+4=10，
∴△AEF的周长为10．

点评本题主要考查等腰三角形的判定和性质，由条件得出BE=DE，DF=CF是解题的关键．

练习册系列答案

世纪百通主体课堂小学课时同步练习系列答案

经纶学典棒棒堂系列答案

16．

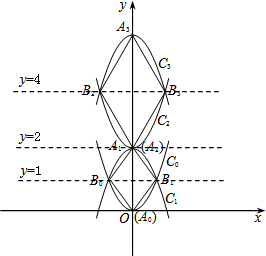如图，已知抛物线C₀：y=x²，顶点记作A₀．首先我们将抛物线C₀关于直线y=1对称翻折过去得到抛物线C₁称为第一次操作，再将抛物线C₁关于直线y=2对称翻折过去得到抛物线C₂称为第二次操作，…，将抛物线C_n-1关于直线y=2^n-1对称翻折过去得到抛物线C_n（顶点记作A_n）称为第n此操作（n=1，2，3…），…．设抛物线C₀与抛物线C₁交于两点B₀与B₁，顺次连接A₀、B₀、A₁、B₁四个点得到四边形A₀B₀A₁B₁，抛物线C₂与抛物线C₃交于两点B₂与B₃，顺次连接A₂、B₂、A₃、B₃四个点得到四边形A₂B₂A₃B₃，…，抛物线C_k-1与抛物线C_k交于两点B_k-1与B_k，顺次连接A_k-1、B_k-1、A_k、B_k四个点得到四边形A_k-1B_k-1A_kB_k（k=1，3，5…），…．
（1）请分别直接写出抛物线C_n（n=1，2，3，4）的解析式；
（2）一系列四边形A_k-1B_k-1A_kB_k（k=1，3，5…）为哪种特殊的四边形（说明理由）？它们都相似吗？如果全都相似，请证明之；如果不全都相似，请举出一对不相似的反例；
（3）试归纳出抛物线C_n的解析式，无需证明．并利用你归纳出来的C_n的解析式，求四边形A_k-1B_k-1A_kB_k（k=1，3，5…）的面积（用含k的式子表示）．

20．已知y=（k-3）x+k-9是关于x的正比例函数．求当x=-4时，y的值．

10．已知直线l经过点M（3，0），N（0，-4），求直线l的解析式．

17．若关于x的不等式（2-m）x≤m-2的解集为x≥-1，则m应满足的条件是（　　）

14．某商店销售每台A型电脑的利润为100元，销售每台B型电脑的利润为150元，该商店计划一次购进A，B两种型号的电脑共100台．
（1）设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y与x的函数关系式；
②该商店计划一次购进A，B两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，那么商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（2）实际进货时，厂家对A型电脑出厂价下调m（50＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（1）中的条件，设计出使这100台电脑销售总利润最大的进货方案．

15．四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是（　　）

试题分类