题目内容
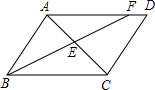
18．
在平行四边形ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，过点O作OE⊥AC，交AD于点E，连接CE，则△CDE的周长为8．
分析 由平行四边形ABCD的对角线相交于点O，OE⊥AC，根据线段垂直平分线的性质，可得AE=CE，又AB+BC=AD+CD=8，继而可得△CDE的周长等于AD+CD．
解答 解：∵四边形ABCD是平行四边形，
∴OA=OC，AB=CD，AD=BC，
∵AB=3，BC=5，
∴AD+CD=8，
∵OE⊥AC，
∴AE=CE，
∴△CDE的周长为：CD+CE+DE=CD+CE+AE=AD+CD=8．
故答案为：8．
点评 此题考查了平行四边形的性质，关键是根据线段垂直平分线的性质进行分析．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
如图，在?ABCD中，AB=2，BC=3，∠ABC的平分线BF分别与AC，AD交于点E，F，则$\frac{{S}_{△AEF}}{{S}_{△BEC}}$=$\frac{4}{9}$．
13．下列说法中，正确的是（ ）
| A． | 方程$\sqrt{x}$=4的根是x=±16 | B． | 方程$\sqrt{3x}$=-x的根是x1=0，x2=3 | ||
| C． | 方程$\sqrt{x+1}$+1=0没有实数根 | D． | 方程3-$\sqrt{2x-3}$的根是x1=2，x2=6 |
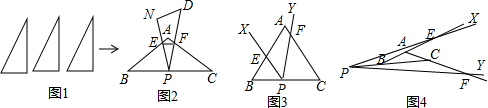
在一条笔直的公路上有A，B，C三地，C地位于A，B两地之间，甲，乙两车分别从A，B两地出发，沿这条公路匀速行驶至C地停止．从甲车出发至甲车到达C地的过程，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图表示，当甲车出发$\frac{3}{2}$h时，两车相距350km．