Question

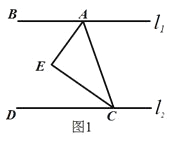
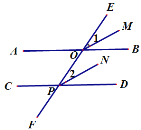
【题目】在△ABC中，D是BC边上的点(不与点B、C重合)，连结AD.

(1)如图1，当点D是BC边上的中点时，S△ABD：S△ACD= ；

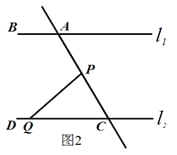
(2)如图2，当AD是∠BAC的平分线时，若AB=m，AC=n，求S△ABD：S△ACD的值(用含m,n的代数式表示)

(3)如图3，AD平分∠BAC，延长AD到E，使得AD=DE，连接BE，如果AC=2，AB=4，S△BDE=6，

那么S△ABC = .

Answer 1

【答案】（1）1:1；（2）m:n；（3）9.

【解析】

（1）过A作AE⊥BC于E，根据三角形面积公式求出即可；

（2）过D作DE⊥AB于E，DF⊥AC于F，根据角平分线性质求出DE=DF，根据三角形面积公式求出即可；

（3）根据已知和（1）（2）的结论求出△ABD和△ACD的面积，即可求出答案．

(1)过A作AE⊥BC于E，

∵点D是BC边上的中点，

∴BD=DC，

∴S△ABD:S△ACD=(×BD×AE):( ×CD×AE)=1:1，

故答案为：1:1；

(2)过D作DE⊥AB于E，DF⊥AC于F，

∵AD为∠BAC的角平分线，

∴DE=DF，

∵AB=m，AC=n，

∴S△ABD:S△ACD=(×AB×DE):(×AC×DF)=m:n；

(3)∵AD=DE，

∴由(1)知：S△ABD:S△EBD=1:1，

∵S△BDE=6，

∴S△ABD=6，

∵AC=2，AB=4，AD平分∠CAB，

∴由(2)知：S△ABD:S△ACD=AB:AC=4:2=2:1，

∴S△ACD=3，

∴S△ABC=3+6=9，

故答案为：9.