题目内容
【题目】如图，直线AB、CD被直线EF所截，交点分别为点O、p，OM平分∠EOB，PN平分∠OPD，如果∠1=∠2，（1）OM∥PN吗？为什么？（2）AB∥CD吗？为什么？
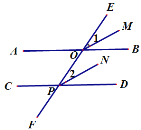
解：（1）OM∥PN．
∵∠1=∠2（ ）．
∴ ∥ ．（ ）
（2）AB∥CD．
∵OM平分∠EOB，PN平分∠OPD（ ）
∴∠EOB= ；∠OPD= （ ）．
又∵∠1=∠2（已知），
∴∠ =∠ （ ），
∴ ∥ ．（ ）
【答案】（1）OM∥PN，理由见解析；（2）AB∥CD，理由见解析
【解析】
（1）根据同位角相等，两直线平行即可判定；
（2）首先由角平分线的性质得出∠EOB=∠OPD，然后根据同位角相等，两直线平行即可判定.
（1）OM∥PN．
∵∠1=∠2（已知），
∴OM∥PN．（同位角相等，两直线平行）
（2）AB∥CD．
∵OM平分∠EOB，PN平分∠OPD（已知）
∴∠EOB=2∠1；∠OPD=2∠2（角平分线的意义）．
又∵∠1=∠2（已知），
∴∠EOB=∠OPD（等式性质），
∴AB∥CD．（同位角相等，两直线平行）
练习册系列答案
阅读快车系列答案
相关题目
