题目内容
6.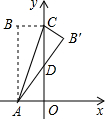 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为(0,2.1).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为(0,2.1).
分析 作B′E⊥x轴,设OD=x,在Rt△AOD中,根据勾股定理列方程,可求得D点的坐标.
解答 解:作B′E⊥x轴,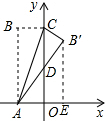
∵∠BAC=∠B′AC,∠BAC=∠OCA,
∴∠B′AC=∠OCA,
∴AD=CD,
设OD=x,AD=5-x,
在Rt△AOD中,根据勾股定理列方程得:22+x2=(5-x)2,
解得:x=2.1,
∴D点的坐标为(0,2.1).
故答案为:(0,2.1).
点评 本题主要考查了折叠的性质、勾股定理,根据勾股定理列方程求出OD是解决问题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
1.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | x2•x3=x6 | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | (x2)3=x6 |
11.-5的绝对值是( )
| A. | -5 | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | 5 |
 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求$\frac{DE}{BC}$的值.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求$\frac{DE}{BC}$的值.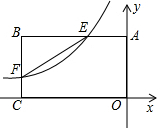 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(-1,2).
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(-1,2).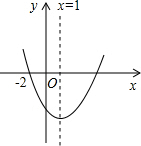 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1),($\frac{7}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1),($\frac{7}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的结论有( )