Question

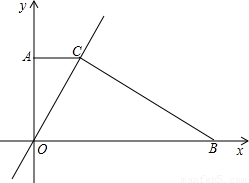
如图，直角梯形AOCD的边OC在x轴上，O为坐标原点，CD垂直于x轴，D（5，4），AD=2．若动点E、F同时从点O出发，E点沿折线OA→AD→DC运动，到达C点时停止；F点沿OC运动，到达C点是停止，它们运动的速度都是每秒1个单位长度．设E运动秒x时，△EOF的面积为y（平方单位），则y关于x的函数图象大致为（ ）

A．
B．
C．
D．

Answer 1

【答案】分析：首先根据点D的坐标求得点A的坐标，从而求得线段OA和线段OC的长，然后根据运动时间即可判断三角形EOF的面积的变化情况．
解答：解：∵D（5，4），AD=2．
∴OC=5，CD=4  OA=5
∴运动x秒（x＜5）时，OE=OF=x，
作EH⊥OC于H，AG⊥OC于点G，
∴EH∥AG
∴△EHO∽△AGO

即：
∴EH=x
∴S△EOF=OF•EH=×x×x=x²，
故A、B选项错误；
当点F运动到点C时，点E运动到点A，此时点F停止运动，点E在AD上运动，△EOF的面积不变，
点在DC上运动时，如右图，
EF=11-x，OC=5
∴S_△EOF=OC•CE=×（11-x）×5=-x+是一次函数，故C正确，
故选C．
点评：本题考查了动点问题的函数图象，解题的关键是根据动点确定分段函数的图象．