��Ŀ����
��2003•����������֪����ͼ��ֱ������ϵ�ڵ�����AOBC��AC��OB��AC��OB�ij��ֱ��ǹ���x�ķ���x2-6mx+m2+4=0������������S��AOC��S��BOC=1��5����1����AC��OB�ij���
��2����BC��OCʱ����OC�ij���OC����ֱ�ߵĽ���ʽ��
��3���ڵڣ�2���ʵ������£��߶�OC���Ƿ����һ��M����M����x���ƽ���ߣ���y����F����BC��D����D����y���ƽ���ߣ���x���ڵ�E��ʹS����FOED=
 S����AOBC�������ڣ���ֱ��д��M������ꣻ�������ڣ�˵�����ɣ�
S����AOBC�������ڣ���ֱ��д��M������ꣻ�������ڣ�˵�����ɣ�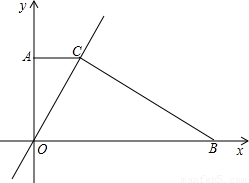
���𰸡���������1�����ݵȸ������ε�������ڵױ߱ȣ��ɵó�AC��OB=1��5����AC��OB���Ƿ���x2-6mx+m2+4=0���������ɸ���Τ�ﶨ���ó�AC��OB�ĺ������ֵ��Ȼ������AC��OB�ı�����ϵʽ�����AC��OB�ij���
��2������Ҫͨ��������������⣮���BC��OC����ô��AOC�͡�OBC��ͬΪ��COB����ǣ����������ȣ��ɵó���OBC�ס�COA���������������εó���OC2=AC•OB�������OC�ij�����������ֱ��������OAC�У����OA�ij�����֪��AC�ij���Ҳ�͵ó���C������꣮���ô���ϵ�������OC����ֱ�ߵĽ���ʽ��
��3�����������FDEO�����S��OE�ij�a�ĺ�����ϵʽ����ֱ֪��BC�Ľ���ʽΪy=- x+
x+ ����ôDE=-
����ôDE=- a+
a+ �����S=OE•DE=-
�����S=OE•DE=- a2+
a2+ a�����������AOBC�����Ϊ6�����S=-
a�����������AOBC�����Ϊ6�����S=- a2+
a2+ a=3�����a=2��3����a=2ʱ��DE=-
a=3�����a=2��3����a=2ʱ��DE=- ×2+
×2+ =
= ����M��������Ϊ
����M��������Ϊ ������ֱ��OC�Ľ���ʽ�пɵ�M��
������ֱ��OC�Ľ���ʽ�пɵ�M�� ��-
��- ����ͬ������õ�a=3ʱ��M��
����ͬ������õ�a=3ʱ��M�� ��1����
��1����
��� �⣺��1����S��AOC��S��BOC=1��5
�⣺��1����S��AOC��S��BOC=1��5
��AC��OB=1��5
������AC=k��OB=5k
�������
��� ��
�� ���������⣬��ȥ��
���������⣬��ȥ��
��AC=1��OB=5��
��2���ߡ�OAC=��BCO=90°����ACO=��BOC
���OBC�ס�COA
�� ��OC2=OB•AC
��OC2=OB•AC
��OC= ��OC=-
��OC=- ����ȥ��
����ȥ��
��AC=1����AO=2
��C��1��2��
��ֱ��OC�Ľ���ʽΪy=2x��
��3�����ڣ�M�� ��
�� ����
���� ��1����
��1����
���������⿼�����һ�κ������ۺ������Լ������Σ����ε����ʣ��Ѷ��еȣ�
��2������Ҫͨ��������������⣮���BC��OC����ô��AOC�͡�OBC��ͬΪ��COB����ǣ����������ȣ��ɵó���OBC�ס�COA���������������εó���OC2=AC•OB�������OC�ij�����������ֱ��������OAC�У����OA�ij�����֪��AC�ij���Ҳ�͵ó���C������꣮���ô���ϵ�������OC����ֱ�ߵĽ���ʽ��
��3�����������FDEO�����S��OE�ij�a�ĺ�����ϵʽ����ֱ֪��BC�Ľ���ʽΪy=-
 x+
x+ ����ôDE=-
����ôDE=- a+
a+ �����S=OE•DE=-
�����S=OE•DE=- a2+
a2+ a�����������AOBC�����Ϊ6�����S=-
a�����������AOBC�����Ϊ6�����S=- a2+
a2+ a=3�����a=2��3����a=2ʱ��DE=-
a=3�����a=2��3����a=2ʱ��DE=- ×2+
×2+ =
= ����M��������Ϊ
����M��������Ϊ ������ֱ��OC�Ľ���ʽ�пɵ�M��
������ֱ��OC�Ľ���ʽ�пɵ�M�� ��-
��- ����ͬ������õ�a=3ʱ��M��
����ͬ������õ�a=3ʱ��M�� ��1����
��1�������
 �⣺��1����S��AOC��S��BOC=1��5
�⣺��1����S��AOC��S��BOC=1��5��AC��OB=1��5
������AC=k��OB=5k
�������

���
 ��
�� ���������⣬��ȥ��
���������⣬��ȥ����AC=1��OB=5��
��2���ߡ�OAC=��BCO=90°����ACO=��BOC
���OBC�ס�COA
��
 ��OC2=OB•AC
��OC2=OB•AC��OC=
 ��OC=-
��OC=- ����ȥ��
����ȥ����AC=1����AO=2
��C��1��2��
��ֱ��OC�Ľ���ʽΪy=2x��
��3�����ڣ�M��
 ��
�� ����
���� ��1����
��1�������������⿼�����һ�κ������ۺ������Լ������Σ����ε����ʣ��Ѷ��еȣ�

��ϰ��ϵ�д�
�����Ŀ
 S����AOBC�������ڣ���ֱ��д��M������ꣻ�������ڣ�˵�����ɣ�
S����AOBC�������ڣ���ֱ��д��M������ꣻ�������ڣ�˵�����ɣ�