题目内容
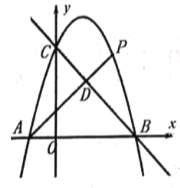
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
(1)求抛物线的解析式和点![]() 的坐标;
的坐标;
(2)![]() 是直线
是直线![]() 上方抛物线上一动点,
上方抛物线上一动点,![]() 交
交![]() 于
于![]() .设
.设![]() ,请求出
,请求出![]() 的最大值和此时点
的最大值和此时点![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,若点
,若点![]() 恰好落在抛物线上,请直接写出此时点
恰好落在抛物线上,请直接写出此时点![]() 的坐标.
的坐标.
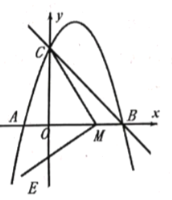
备用图
【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)把点B(3,0)代入![]() 先求得c的值,再求得点C的坐标,利用待定系数法即可求得抛物线的解析式和点A的坐标;
先求得c的值,再求得点C的坐标,利用待定系数法即可求得抛物线的解析式和点A的坐标;
(2)设点P的横坐标为![]() ,作
,作![]() 轴于N,交BC于M,先用m表示出
轴于N,交BC于M,先用m表示出![]() ,再作
,再作![]() 于E,
于E,![]() 于F,得到
于F,得到![]() ,即
,即![]() ,推出
,推出![]() ,得到
,得到 ,利用二次函数的性质即可求解;
,利用二次函数的性质即可求解;
(3)过M,E分别作![]() 轴,
轴,![]() 轴的垂线交于H,设点M的坐标为(
轴的垂线交于H,设点M的坐标为(![]() ,
,![]() ),证得
),证得![]() ,得到点E的坐标为(
,得到点E的坐标为(![]() ,
,![]() ),代入
),代入![]() 即可得n的值,即可求解.
即可得n的值,即可求解.
(1)∵![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点C,
轴交于点C,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵抛物线![]() 经过点B,C,
经过点B,C,
∴![]()
解得![]() ,
,
∴抛物线解析式为![]() ;
;
当![]() 时,
时,![]() ,
,
解得:![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)设点P的横坐标为![]() ,连接PC,PB,过P作
,连接PC,PB,过P作![]() 轴于N,交BC于M,
轴于N,交BC于M,
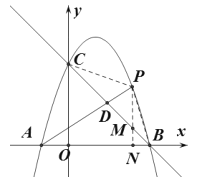
由(1)知:直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
连接AC,分别过A,P作![]() 于E,
于E,![]() 于F,
于F,
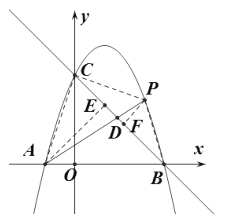
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴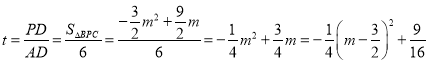 ,
,
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ;
;
(3)过M,E分别作![]() 轴,
轴,![]() 轴的垂线交于H,
轴的垂线交于H,
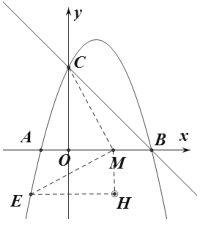
∴∠H=90![]() ,∠MEH=∠OME,
,∠MEH=∠OME,
根据旋转的性质知:∠CME=90![]() ,EM=MC,
,EM=MC,
∴∠CMO+∠OME=90![]() ,∠CMO+∠MCO=90
,∠CMO+∠MCO=90![]() ,
,
∴∠MEH=∠MCO,
设点M的坐标为(![]() ,
,![]() ),
),
根据题意将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,若点
,若点![]() 恰好落在抛物线上,
恰好落在抛物线上,
则点M在![]() 轴正半轴上,即
轴正半轴上,即![]() ,
,
在Rt△MEH和Rt△MCO中,
 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点E的坐标为:(![]() ,
,![]() ),
),
把代入E (![]() ,
,![]() ) 代入
) 代入![]() ,
,
整理得:![]() ,
,
解得![]() ,
,![]() .
.
∴点M的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) | 1 | 2 | 4 | 7 | 11 | 12 |
y(斤) | 0.75 | 1.00 | 1.50 | 2.75 | 3.25 | 3.50 |
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
【题目】某校组织了一次创建全国文明城市知识竞赛活动,有30名同学参加这次竞赛,成绩分布频数表如下:(单位:分)
成绩(分) | 组中值 | 频数(人数) |
80.5~85.5 | 83 | 3 |
85.5~90.5 | 88 | 6 |
90.5~95.5 | 93 | 12 |
95.5~100.5 | 98 | 9 |
(1)利用组中值计算这30位同学的平均数;
(2)学校根据这次竞赛成绩从高到低选15位同学参加市级比赛,小明同学也参加了这次竞赛,知道自己的成绩后,他想知道自己是否有资格参加市里比赛(学校还未公布到市里比赛名单),他最应关注频数,平均分,众数,中位数中的哪个量?请说明理由;
(3)“创文知识竞赛”中,获一等奖的小红同学得到了印有龚扇、剪纸、彩灯图案的三枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有彩灯图案的概率是多少?请用树状图或列表法说明.