题目内容
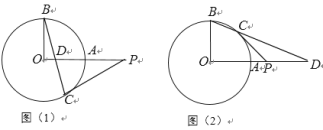
【题目】平面直角坐标系中，四边形OABC是正方形，点A，C 在坐标轴上，点B（
，），P是射线OB上一点，将
绕点A顺时针旋转90°，得
，Q是点P旋转后的对应点.
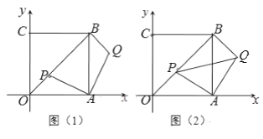
（1）如图（1）当OP = 
时，求点Q的坐标；
（2）如图（2），设点P（
，
）（
），
的面积为S. 求S与的函数关系式，并写出当S取最小值时，点P的坐标；
（3）当BP+BQ = 
时，求点Q的坐标（直接写出结果即可）
【答案】（1）
；（2）
，
；（3）
．
【解析】
（1）先根据正方形的性质、解直角三角形可得
，
，再根据三角形全等的判定定理与性质可得
，从而可得
，由此即可得出答案；
（2）先根据正方形的性质得出
，
，再根据旋转的性质、勾股定理可得
，
，然后根据直角三角形的面积公式可得S与x的函数关系式，最后利用二次函数的解析式即可得点P的坐标；
（3）先根据旋转的性质、正方形的性质得出
，
，从而得出点P在OB的延长线上，再根据线段的和差可得
，然后同（1）的方法可得
，
，最后根据三角形全等的性质、线段的和差可得
，由此即可得出答案．
（1）如图1，过P点作
轴于点G，过Q点作
轴于点H
∵四边形OABC是正方形
∴
∵
∴
在
中，
，
∴
∵
绕点A顺时针旋转
得到
∴
，
在
和
中，
∴
∴
∴
则点Q的坐标为；
（2）如图2，过P点作轴于点G
∵绕点A顺时针旋转得到
∴
∵
∴，
∴
在
中，由勾股定理得：
整理得：
∴
整理得：
由二次函数的性质可知，当
时，S随x的增大而减小；当
时，S随x的增大而增大
则当
时，S取得最小值，最小值为9
此时
故点P的坐标为；
（3）∵绕点A顺时针旋转得到
∴
∵
∴
∵四边形OABC是正方形，且边长
对角线
∴点P在OB的延长线上
∴
解得
如图3，过P点作轴于点G，过Q点作轴于点H
同（1）可得：，
，
则点Q的坐标为．
练习册系列答案
相关题目
